
【题目】如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)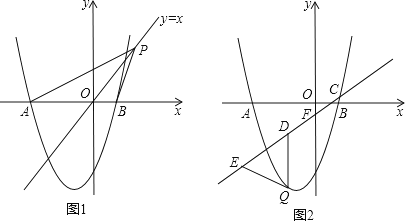
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y= ![]() x﹣
x﹣ ![]() 分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
【答案】
(1)
解:把B(1,0)代入y=ax2+2x﹣3,
可得a+2﹣3=0,解得a=1,
∴抛物线解析式为y=x2+2x﹣3,
令y=0,可得x2+2x﹣3=0,解得x=1或x=﹣3,
∴A点坐标为(﹣3,0).
(2)
解:若y=x平分∠APB,则∠APO=∠BPO,
如图1,若P点在x轴上方,PA与y轴交于点B′,
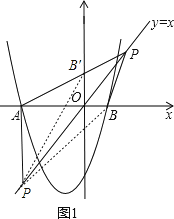
由于点P在直线y=x上,可知∠POB=∠POB′=45°,
在△BPO和△B′PO中
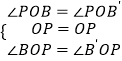 ,
,
∴△BPO≌△B′PO(ASA),
∴BO=B′O=1,
设直线AP解析式为y=kx+b,把A、B′两点坐标代入可得
![]() ,解得
,解得 ![]() ,
,
∴直线AP解析式为y= ![]() x+1,
x+1,
联立 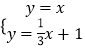 ,解得
,解得 ![]() ,
,
∴P点坐标为( ![]() ,
, ![]() );
);
若P点在x轴下方时,同理可得△BOP≌△B′OP,
∴∠BPO=∠B′PO,
又∠B′PO在∠APO的内部,
∴∠APO≠∠BPO,即此时没有满足条件的P点,
综上可知P点坐标为( ![]() ,
, ![]() ).
).
(3)
解:如图2,作QH⊥CF,交CF于点H,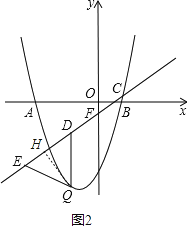
∵CF为y= ![]() x﹣
x﹣ ![]() ,
,
∴可求得C( ![]() ,0),F(0,﹣
,0),F(0,﹣ ![]() ),
),
∴tan∠OFC= ![]() =
= ![]() ,
,
∵DQ∥y轴,
∴∠QDH=∠MFD=∠OFC,
∴tan∠HDQ= ![]() ,
,
不妨设DQ=t,DH= ![]() t,HQ=
t,HQ= ![]() t,
t,
∵△QDE是以DQ为腰的等腰三角形,
∴若DQ=DE,则S△DEQ= ![]() DEHQ=
DEHQ= ![]() ×
× ![]() t×t=
t×t= ![]() t2,
t2,
若DQ=QE,则S△DEQ= ![]() DEHQ=
DEHQ= ![]() ×2DHHQ=
×2DHHQ= ![]() ×
× ![]() t×
t× ![]() t=
t= ![]() t2,
t2,
∵ ![]() t2<
t2< ![]() t2,
t2,
∴当DQ=QE时△DEQ的面积比DQ=DE时大.
设Q点坐标为(x,x2+2x﹣3),则D(x, ![]() x﹣
x﹣ ![]() ),
),
∵Q点在直线CF的下方,
∴DQ=t= ![]() x﹣
x﹣ ![]() ﹣(x2+2x﹣3)=﹣x2﹣
﹣(x2+2x﹣3)=﹣x2﹣ ![]() x+
x+ ![]() ,
,
当x=﹣ ![]() 时,tmax=3,
时,tmax=3,
∴(S△DEQ)max= ![]() t2=
t2= ![]() ,
,
即以QD为腰的等腰三角形的面积最大值为 ![]()
【解析】(1)把B点坐标代入抛物线解析式可求得a的值,可求得抛物线解析式,再令y=0,可解得相应方程的根,可求得A点坐标;
(2)当点P在x轴上方时,连接AP交y轴于点B′,可证△OBP≌△OB′P,可求得B′坐标,利用待定系数法可求得直线AP的解析式,联立直线y=x,可求得P点坐标;当点P在x轴下方时,同理可求得∠BPO=∠B′PO,又∠B′PO在∠APO的内部,可知此时没有满足条件的点P;
(3)过Q作QH⊥DE于点H,由直线CF的解析式可求得点C、F的坐标,结合条件可求得tan∠QDH,可分别用DQ表示出QH和DH的长,分DQ=DE和DQ=QE两种情况,分别用DQ的长表示出△QDE的面积,再设出点Q的坐标,利用二次函数的性质可求得△QDE的面积的最大值. 本题主要考查二次函数的综合应用,涉及知识点有待定系数法、角平分线的定义、全等三角形的判定和性质、三角形的面积、等腰三角形的性质、二次函数的性质及分类讨论等.在(2)中确定出直线AP的解析式是解题的关键,在(3)中利用DQ表示出△QDE的面积是解题的关键.本题考查知识点较多,综合性较强,计算量大,难度较大.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)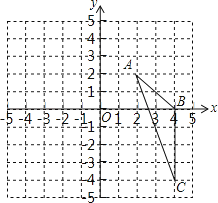
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的 ![]() ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=3,BC=4,点O是BC中点,将△ABC绕点O旋转得△A′B' C′,则在旋转过程中点A、C′两点间的最大距离是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将ABCO绕点A逆时针旋转得到ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点D在反比例函数y= ![]() (x<0)的图象上,则k的值为
(x<0)的图象上,则k的值为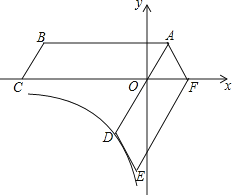
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)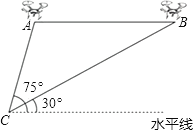
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是1.请同学们利用网格线进行画图:
(1)在图1中,画一个顶点为格点、面积为5的正方形;
(2)在图2中,已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形;(要求画出所有符合题意的线段)
(3)在图3中,找一格点D,满足:①到CB、CA的距离相等;②到点A、C的距离相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校的复印任务原来由甲复印社承接,其收费y(元)与复印页数x(页)的关系如下表:
x(页) | 100 | 200 | 400 | 1000 | … |
y(元) | 40 | 80 | 160 | 400 |
(1)若y与x满足初中学过的某一函数关系,求函数的解析式;
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费,则乙复印社每月收费y(元)与复印页数x(页)的函数关系为________________,
(3)学校准备复印材料1000页,应选择哪个复印社比较优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com