
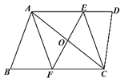
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连接AF、CE.试判断四边形AECF的形状,并证明.
科目:初中数学 来源: 题型:
【题目】在⊙O中按如下步骤作图:
(1)作⊙O的直径AD;
(2)以点D为圆心,DO长为半径画弧,交⊙O于B,C两点;
(3)连接DB,DC,AB,AC,BC.
根据以上作图过程及所作图形,下列四个结论中错误的是( )
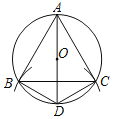
A.∠ABD=90°B.∠BAD=∠CBDC.AD⊥BCD.AC=2CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (b,c为常数)经过点
(b,c为常数)经过点![]() .
.
(1)求抛物线的解析式;
(2)设该抛物线与x轴的另一个交点为C,其顶点为D,求点C,D的坐标,并判断![]() 形状;
形状;
(3)点P是直线![]() 上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线
上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线![]() 上,距离点P为
上,距离点P为![]() 个单位长度.设点P的横坐标为t,
个单位长度.设点P的横坐标为t,![]() 的面积为S,求S与t之间的函数关系式.
的面积为S,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于新冠肺炎疫情的影响,市场上防护口罩出现热销,某口罩厂每月固定生产甲、乙两种型号的防护口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表所示:
甲 | 乙 | |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过218万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入-投入总成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
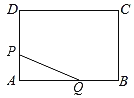
【题目】如图,矩形ABCD的周长是28cm,且AB比BC长2cm.若点P从点A出发,以1cm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止运动.若设运动时间为t(s),△APQ的面积为S(cm2),则S(cm2)与t(s)之间的函数图象大致是( )
A.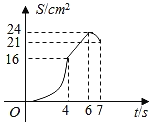 B.
B.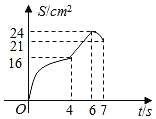 C.
C.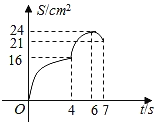 D.
D.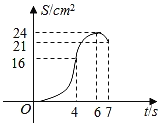
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
(1)P点的坐标为多少;(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com