
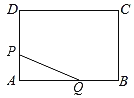
【题目】如图,矩形ABCD的周长是28cm,且AB比BC长2cm.若点P从点A出发,以1cm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止运动.若设运动时间为t(s),△APQ的面积为S(cm2),则S(cm2)与t(s)之间的函数图象大致是( )
A.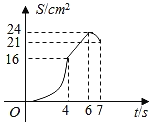 B.
B. C.
C. D.
D.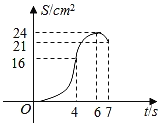
【答案】A
【解析】
分0≤t≤4、4<t≤6、6<t≤7分别求出函数表达式,即可求解.
解:由题意得:AD+AD+2=14,
解得:AD=6,则AB=8,
(1)当0≤t≤4时,如图1,
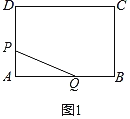
S=![]() AP×AQ=
AP×AQ=![]() ×t×2t=t2,
×t×2t=t2,
该函数为开口向上的抛物线,当t=4时,S=16;
(2)当4<t≤6时,如图2,
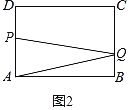
点P在AD、点Q在BC,
则AP=t,
S=![]() ×AP×AB=
×AP×AB=![]() ×t×8=4t,
×t×8=4t,
该函数为一次函数,当t=6时,S=24;
(3)当6<t≤7时,如图3,
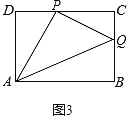
点P在CD上,点Q在BC上,
则PD=t﹣6,PC=14﹣t,BQ=2t﹣8,CQ=14﹣2t,
S=S矩形ABCD﹣[S△APD+S△ABQ+S△PQC]=6×8﹣[![]() ×(14﹣t)(14﹣2t)+
×(14﹣t)(14﹣2t)+![]() ×6×(t﹣6)+
×6×(t﹣6)+![]() ×8×(2t﹣8)]=﹣t2+10t,
×8×(2t﹣8)]=﹣t2+10t,
该函数为开口向下的抛物线,当t=7时,S=21;
故选:A.


科目:初中数学 来源: 题型:
【题目】实行垃圾分类和垃圾资源化利用,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.某环保公司研发了甲、乙两种智能设备,可利用最新技术将干垃圾进行分选破碎制成固化成型燃料棒,干垃圾由此变身新型清洁燃料.某垃圾处理厂从环保公司购入以上两种智能设备若干,已知购买甲型智能设备花费![]() 万元,购买乙型智能设备花费
万元,购买乙型智能设备花费![]() 万元,购买的两种设备数量相同,且两种智能设备的单价和为
万元,购买的两种设备数量相同,且两种智能设备的单价和为![]() 万元.
万元.
![]() 求甲、乙两种智能设备单价;
求甲、乙两种智能设备单价;
![]() 垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的
垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的![]() ,且生产每吨燃料棒所需人力成本比物资成本的倍
,且生产每吨燃料棒所需人力成本比物资成本的倍![]() 还多
还多![]() 元.调查发现,若燃料棒售价为每吨
元.调查发现,若燃料棒售价为每吨![]() 元,平均每天可售出
元,平均每天可售出![]() 吨,而当销售价每降低
吨,而当销售价每降低![]() 元,平均每天可多售出
元,平均每天可多售出![]() 吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到
吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到![]() 元,且保证售价在每吨
元,且保证售价在每吨![]() 元基础上降价幅度不超过
元基础上降价幅度不超过![]() ,求每吨燃料棒售价应为多少元?
,求每吨燃料棒售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③三次函数
;③三次函数![]() 的图象与x轴交点的横坐标分别为a和b,则
的图象与x轴交点的横坐标分别为a和b,则![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连接AF、CE.试判断四边形AECF的形状,并证明.
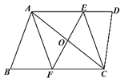
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
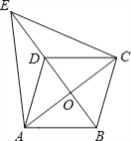
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清代《修武县志》有胜果寺的记载,“康熙五十二年三月十七日,塔顶现青白二气如云,越二日乃止”,此文中的塔即为“胜果寺塔”,是修武作为“千年古县”的标志性古建筑.为了测量塔的高度,某校数学兴趣小组的两名同学采用了如下方式进行测量.如图,小明站在![]() 处,眼睛
处,眼睛![]() 距离地面的高度为
距离地面的高度为![]() ,测得塔顶
,测得塔顶![]() 的仰角为
的仰角为![]() ,小红站在距离小明
,小红站在距离小明![]() 的
的![]() 处,眼睛
处,眼睛![]() 距离地面的高度为
距离地面的高度为![]() ,测得塔顶
,测得塔顶![]() 的仰角为
的仰角为![]() ,已知
,已知![]() ,
,![]() ,塔底
,塔底![]() 在同一水平面上,由此即可求出塔高
在同一水平面上,由此即可求出塔高![]() .你知道是怎么求的吗?请写出解题过程.(结果精确到
.你知道是怎么求的吗?请写出解题过程.(结果精确到![]() .参考数据:
.参考数据:![]() )
)
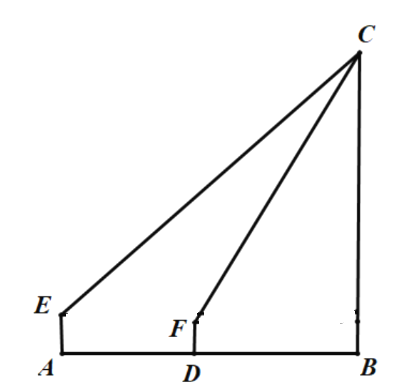
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的点阵图,探究其中的规律.
摆第1个“小屋子”需要5个点,
摆第2个“小屋子”需要 个点,摆第3个“小屋子”需要 个点?
(1)摆第10个这样的“小屋子”需要多少个点?
(2)写出摆第n个这样的“小屋子”需要的总点数,S与n的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生零用钱支出情况,从七、八、九年级800名学生中随机抽取部分学生,对他们今年5月份的零用钱支出情况进行调查统计,并绘制成如下统计图表:
组别 | 零用钱支出x(单位:元) | 频数(人数) | 频率 | |
节俭型 | 一 | x<20 | m | 0.05 |
二 | 20≤x<30 | 4 | a | |
富足型 | 三 | 30≤x<40 | n | 0.45 |
四 | 40≤x<50 | 12 | b | |
奢侈型 | 五 | x≥50 | 4 | c |
合计 | 1 | |||
(1)表中a+b+c= ;m= ;本次调查共随机抽取了 名同学;
(2)在扇形统计图中,“富足型”对应的扇形的圆心角的度数是 ;
(3)估计今年5月份全校零花钱支出在30≤x<40范围内的学生人数;
(4)在抽样的“奢侈型”学生中,有2名女生和2名男生.学校团委计划从中随机抽取2名同学参加“绿苗理财计划”活动,请运用树状图或者列表说明恰好抽到一男一女的概率.
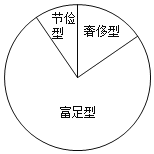
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图①,![]() 是等腰直角三角形,四边形
是等腰直角三角形,四边形![]() 是正方形,点
是正方形,点![]() 与点
与点![]() 重合,则线段
重合,则线段![]() 与
与![]() 之间的数量关系和位置关系分别是 .
之间的数量关系和位置关系分别是 .
(2)深入探究
如图②,![]() 是等腰直角三角形,四边形
是等腰直角三角形,四边形![]() 是正方形,点
是正方形,点![]() 在直线
在直线![]() 上,对角线
上,对角线![]() 所在的直线交直线
所在的直线交直线![]() 于点
于点![]() ,则线段
,则线段![]() 之间有什么数量关系?请仅就图②给出证明.
之间有什么数量关系?请仅就图②给出证明.
(3)拓展思维
如图②,若点![]() 在直线
在直线![]() 上,且线段
上,且线段![]() ,当
,当![]() 时,直接写出此时正方形
时,直接写出此时正方形![]() 的面积.
的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com