
【题目】观察下面的点阵图,探究其中的规律.
摆第1个“小屋子”需要5个点,
摆第2个“小屋子”需要 个点,摆第3个“小屋子”需要 个点?
(1)摆第10个这样的“小屋子”需要多少个点?
(2)写出摆第n个这样的“小屋子”需要的总点数,S与n的关系式.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是![]()
![]()
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于新冠肺炎疫情的影响,市场上防护口罩出现热销,某口罩厂每月固定生产甲、乙两种型号的防护口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表所示:
甲 | 乙 | |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过218万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入-投入总成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的周长是28cm,且AB比BC长2cm.若点P从点A出发,以1cm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止运动.若设运动时间为t(s),△APQ的面积为S(cm2),则S(cm2)与t(s)之间的函数图象大致是( )
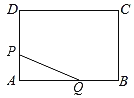
A.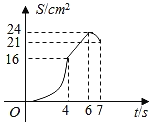 B.
B.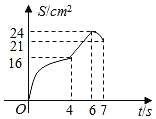 C.
C.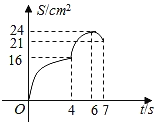 D.
D.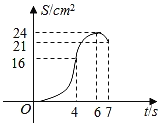
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南灵宝苹果为中华苹果之翘楚,被誉为“中华名果”.某水果超市计划从灵宝购进“红富士”与“新红星”两种品种的苹果.已知2箱红富士苹果的进价与3箱新红星苹果的进价的和为282元,且每箱红富士苹果的进价比每箱新红星苹果的进价贵6元.
(1)求每箱红富士苹果的进价与每箱新红星苹果的进价分别是多少元?
(2)如果购进红富士苹果有优惠,优惠方案是:购进红富士苹果超过20箱,超出部分可以享受七折优惠.若购进![]() (
(![]() ,且
,且![]() 为整数)箱红富士苹果需要花费
为整数)箱红富士苹果需要花费![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,超市决定在红富士、新红星两种苹果中选购其中一种,且数量超过20箱,请你帮助超市选择购进哪种苹果更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
(1)P点的坐标为多少;(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),与y轴的交点为C,已知﹣2≤c≤﹣1,顶点坐标为(1,n),则下列结论正确的是( )

A.a+b>0
B.![]()
C.对于任意实数m,不等式a+b>am2+bm恒成立
D.关于x的方程ax2+bx+c=n+1没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 与正比例函数
与正比例函数![]() 交于格点(网格线的交点)
交于格点(网格线的交点)![]() .
.
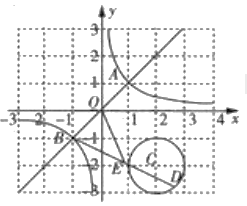
(1)填空:![]() ;
;![]() ;
;
(2)当![]() 时,直接写出
时,直接写出![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)点![]() 是以格点
是以格点![]() 为圆心,
为圆心, ![]() 为半径的圆上一动点,连接
为半径的圆上一动点,连接![]() 取
取![]() 的中点
的中点![]() 试确定线段
试确定线段![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1,x2,当k=1时,求x12+x22的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com