
【题目】已知抛物线![]() (b,c为常数)经过点
(b,c为常数)经过点![]() .
.
(1)求抛物线的解析式;
(2)设该抛物线与x轴的另一个交点为C,其顶点为D,求点C,D的坐标,并判断![]() 形状;
形状;
(3)点P是直线![]() 上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线
上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线![]() 上,距离点P为
上,距离点P为![]() 个单位长度.设点P的横坐标为t,
个单位长度.设点P的横坐标为t,![]() 的面积为S,求S与t之间的函数关系式.
的面积为S,求S与t之间的函数关系式.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,直角三角形;(3)当点M在点P下方时,
,直角三角形;(3)当点M在点P下方时,![]() ,当点M在点P上方时,
,当点M在点P上方时,![]() (
(![]() 或
或![]() )
)
【解析】
(1)利用待定系数法即可求得答案;
(2)将二次函数关系式配成顶点式即可求得顶点D的坐标,令y=0即可求得点C的坐标,最后利用该勾股定理及其逆定理即可判断![]() 的形状;
的形状;
(3)过点Q作![]() 于点G.先求得
于点G.先求得![]() ,再根据点P的位置分类讨论,画出相应图形计算即可.
,再根据点P的位置分类讨论,画出相应图形计算即可.
解:(1)∵抛物线过![]() 两点,
两点,
∴![]()
解得![]()
∴抛物线解析式为![]() ;
;
(2)由![]() ,得点D的坐标为
,得点D的坐标为![]() .
.
当![]() 时,
时,![]() ,
,
解得![]() .
.
∴点C的坐标为![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∴![]() 为直角三角形.
为直角三角形.
(3)过点Q作![]() 于点E.
于点E.
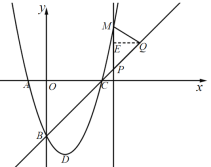
∵![]() 轴,
轴,
∴![]() .
.
∵![]() ,
,
∴![]() ,直线
,直线![]() 的解析式为
的解析式为![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
①当点M在点P下方时,![]() ,
,
∴![]() .
.
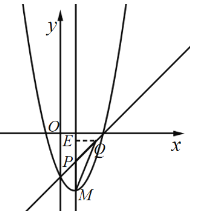
②当点M在点P上方时,![]() ,
,
∴![]() (
(![]() 或
或![]() )
)


科目:初中数学 来源: 题型:
【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,结果有“好评”“中评”“差评”三种评价.假设这三种评价是等可能的,小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图,利用图中所提供的信息解决以下问题:

(1)请将图1补充完整;
(2)图2中“差评”所占扇形圆心角的度数是___;
(3)若甲、乙两名消费者在该网店购买了同一商品,请你用表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
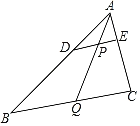
【题目】如图所示,在△ABC中,DE∥BC,AD=5,BD=10,AE=3.
(1)求CE的长.
(2)在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.小明认为![]() ,你认为小明的结论正确吗?请说明你的理由.
,你认为小明的结论正确吗?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
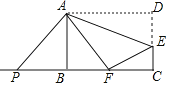
【题目】如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③三次函数
;③三次函数![]() 的图象与x轴交点的横坐标分别为a和b,则
的图象与x轴交点的横坐标分别为a和b,则![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________![]() ;
;
(2)请补全条形统计图;
(3)若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为![]() ,现从中随机抽取
,现从中随机抽取![]() 人参加食品安全知识竞赛,则恰好抽到
人参加食品安全知识竞赛,则恰好抽到![]() 个男生和
个男生和![]() 个女生的概率________.
个女生的概率________.
查看答案和解析>>
科目:初中数学 来源: 题型:
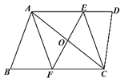
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连接AF、CE.试判断四边形AECF的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
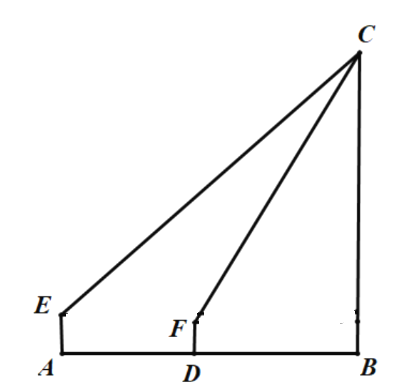
【题目】清代《修武县志》有胜果寺的记载,“康熙五十二年三月十七日,塔顶现青白二气如云,越二日乃止”,此文中的塔即为“胜果寺塔”,是修武作为“千年古县”的标志性古建筑.为了测量塔的高度,某校数学兴趣小组的两名同学采用了如下方式进行测量.如图,小明站在![]() 处,眼睛
处,眼睛![]() 距离地面的高度为
距离地面的高度为![]() ,测得塔顶
,测得塔顶![]() 的仰角为
的仰角为![]() ,小红站在距离小明
,小红站在距离小明![]() 的
的![]() 处,眼睛
处,眼睛![]() 距离地面的高度为
距离地面的高度为![]() ,测得塔顶
,测得塔顶![]() 的仰角为
的仰角为![]() ,已知
,已知![]() ,
,![]() ,塔底
,塔底![]() 在同一水平面上,由此即可求出塔高
在同一水平面上,由此即可求出塔高![]() .你知道是怎么求的吗?请写出解题过程.(结果精确到
.你知道是怎么求的吗?请写出解题过程.(结果精确到![]() .参考数据:
.参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在九年级“线上教学”结束后,为了了解学生的视力情况,抽查了部分学生进行视力检查.根据检查结果,制作下面不完整的统计图表.

(1)求组别C的频数m的值.
(2)求组别A的圆心角度数.
(3)如果势视力值4.8及以上属于“视力良好”,请估计该市25000名九年级学生达到“视力良好”的人数,根据上述图表信息,你对视力保护有什么建议?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com