
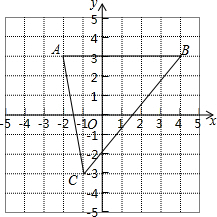
 如图,已知A(-2,3)、B(4,3)、C(-1,-3)
如图,已知A(-2,3)、B(4,3)、C(-1,-3)分析 (1)点C的纵坐标的绝对值就是点C到x轴的距离解答;
(2)根据三角形的面积公式列式进行计算即可求解;
(3)设点P的坐标为(0,y),根据△ABP的面积为6,A(-2,3)、B(4,3),所以$\frac{1}{2}×6×|x-3|=6$,即|x-3|=2,所以x=5或x=1,即可解答.
解答 解:(1)∵C(-1,-3),
∴|-3|=3,
∴点C到x轴的距离为3;
(2)∵A(-2,3)、B(4,3)、C(-1,-3)
∴AB=4-(-2)=6,点C到边AB的距离为:3-(-3)=6,
∴△ABC的面积为:6×6÷2=18.
(3)设点P的坐标为(0,y),
∵△ABP的面积为6,A(-2,3)、B(4,3),
∴$\frac{1}{2}×$6×|y-3|=6,
∴|y-3|=2,
∴y=1或y=5,
∴P点的坐标为(0,1)或(0,5).
点评 本题考查了坐标与图形,解决本题的关键是利用数形结合的思想.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | πcm2 | B. | 2πcm2 | C. | 3πcm2 | D. | 6πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
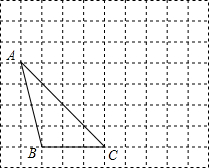 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5个单位得△A1B1C1,再向上平移2个单位得△A2B2C2.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5个单位得△A1B1C1,再向上平移2个单位得△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
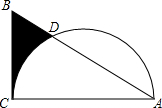 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC为直径作半圆交AB于点D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC为直径作半圆交AB于点D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
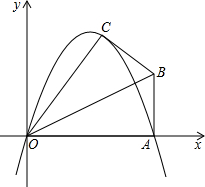 如图,抛物线$y=-\frac{2}{3}{x^2}+\frac{10}{3}x$的图象与x轴交于A点,过A作BA⊥OA,点B在第一象限内,将Rt△OAB沿OB折叠后,使点A落在点C处,且tan∠COA=$\frac{4}{3}$.
如图,抛物线$y=-\frac{2}{3}{x^2}+\frac{10}{3}x$的图象与x轴交于A点,过A作BA⊥OA,点B在第一象限内,将Rt△OAB沿OB折叠后,使点A落在点C处,且tan∠COA=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
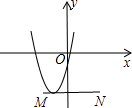 如图,线段MN在平面直角坐标系中,点M,N的坐标分别为(-2,-4),(3,-4),抛物线y=ax2+bx+c(a>0)顶点在线段MN上运动,该抛物线与x轴交于点C,D(点C在点D的左侧),下列结论中:①c≥-3;②当x>4时,y随x的增大而增大;③若点C的横坐标的最小值为-4,则点D的横坐标最小值为0,其中正确的有( )
如图,线段MN在平面直角坐标系中,点M,N的坐标分别为(-2,-4),(3,-4),抛物线y=ax2+bx+c(a>0)顶点在线段MN上运动,该抛物线与x轴交于点C,D(点C在点D的左侧),下列结论中:①c≥-3;②当x>4时,y随x的增大而增大;③若点C的横坐标的最小值为-4,则点D的横坐标最小值为0,其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com