
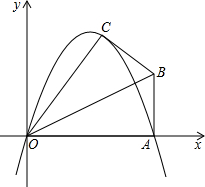
 ��ͼ��������$y=-\frac{2}{3}{x^2}+\frac{10}{3}x$��ͼ����x�ύ��A�㣬��A��BA��OA����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���ʹ��A���ڵ�C������tan��COA=$\frac{4}{3}$��
��ͼ��������$y=-\frac{2}{3}{x^2}+\frac{10}{3}x$��ͼ����x�ύ��A�㣬��A��BA��OA����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���ʹ��A���ڵ�C������tan��COA=$\frac{4}{3}$������ ��1������C��CD��x���ڵ�D���������A�����꣬�����ù��ɶ����ó�C�����꣬�����ó��𰸣�
��2������ȷ��OC�Ľ���ʽ������ȷ��ƽ����OC��ֱ�߽���ʽ��Ȼ����������ʽ���ó�����m�ķ��̣������б�ʽΪ0���m��ֵ�������á�OCD��������⣬�ɵý��ۣ�
��3���ȵó���y��Ľ�������Ϊ��0��2����0��-2��������ֱ��AP�Ľ���ʽ�����������߽���ʽ�������ⷽ����ɵõ�P�����꣮
��� �⣺��1����ͼ��ʾ������C��CD��x���ڵ�D��
��������$y=-\frac{2}{3}{x^2}+\frac{10}{3}x$��ͼ����x�ύ��A�㣬
��0=-$\frac{2}{3}$x2+$\frac{10}{3}$x��
��ã�x1=0��x2=5��
��A��5��0����
�֡�tan��COA=$\frac{4}{3}$��AC=AO=5��
��DC=4��OD=3��
��C��3��4����
��x=3ʱ��y=-$\frac{2}{3}$x2+$\frac{10}{3}$x=4��
���C���������ϣ�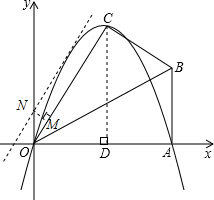
��2����C��3��4����
��ֱ��OC�Ľ���ʽΪy=$\frac{4}{3}$x��
���M��OC��������ʱ��ƽ����OC��ֱ�߽���ʽΪy=$\frac{4}{3}$x+m��
����$\left\{\begin{array}{l}{y=\frac{4}{3}x+m}\\{y=-\frac{2}{3}{x}^{2}+\frac{10}{3}x}\end{array}\right.$��
����δ֪��y�������ã�2x2-6x+3m=0��
��=��-6��2-24m=0��
��ã�m=$\frac{3}{2}$��
���M��OC��������Ϊx��
�ߡ�NOM=��OCD��
��sin��OCD=sin��NOM=$\frac{3}{5}$��
��$\frac{x}{\frac{3}{2}}$=$\frac{3}{5}$��
��ã�x=$\frac{9}{10}$��
��3���ߡ�OAP=��BOA��
��OP=OA��
����y��Ľ�������Ϊ��0��2����0��-2����
��ֱ��AP�����㣨2$\sqrt{3}$��0������0��2��ʱ������ʽΪ��y=-$\frac{\sqrt{3}}{3}$x+2��
����$\left\{\begin{array}{l}{y=-{x}^{2}+2\sqrt{3}}\\{y=-\frac{\sqrt{3}}{3}x+2}\end{array}\right.$��
���$\left\{\begin{array}{l}{{x}_{1}=2\sqrt{3}}\\{{y}_{1}=0}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=\frac{\sqrt{3}}{3}}\\{{y}_{2}=\frac{5}{3}}\end{array}\right.$��
���Ե�P������Ϊ��$\frac{\sqrt{3}}{3}$��$\frac{5}{3}$����
��ֱ��AP�����㣨2$\sqrt{3}$��0������0��-2��ʱ������ʽΪy=$\frac{\sqrt{3}}{3}$x-2��
����$\left\{\begin{array}{l}{y=-{x}^{2}+2\sqrt{3}}\\{y=\frac{\sqrt{3}}{3}x-2}\end{array}\right.$��
���$\left\{\begin{array}{l}{{x}_{1}=2\sqrt{3}}\\{{y}_{1}=0}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=\frac{\sqrt{3}}{3}}\\{{y}_{2}=-\frac{7}{3}}\end{array}\right.$��
�Ե�P������Ϊ��-$\frac{\sqrt{3}}{3}$��-$\frac{7}{3}$����
��������������һ�㣨$\frac{\sqrt{3}}{3}$��$\frac{5}{3}$����-$\frac{\sqrt{3}}{3}$��-$\frac{7}{3}$����ʹ��OAP=��BOA��
���� ���⿼���˶��κ������ۺ�Ӧ�ã��漰��ͼ�εķ��۱任�����ô���ϵ������һ�κ��������κ����Ľ���ʽ��ֱ���������ߵĽ������֪ʶ������һ�����ۺ������Ѷȣ�����ʱҪע�����ν��˼���뷽��˼���Ӧ�ã�


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
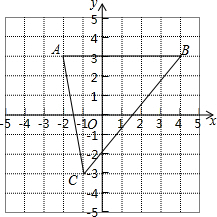 ��ͼ����֪A��-2��3����B��4��3����C��-1��-3��
��ͼ����֪A��-2��3����B��4��3����C��-1��-3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
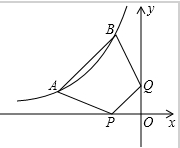 ��ͼ��A��a��1����B��-1��b������˫����y=-$\frac{3}{x}$��x��0����P��Q�ֱ���x�ᣬy���ϵĶ��㣬���ı���PABQ���ܳ���Сֵʱ��PQ����ֱ�ߵĽ���ʽ��y=x+2��
��ͼ��A��a��1����B��-1��b������˫����y=-$\frac{3}{x}$��x��0����P��Q�ֱ���x�ᣬy���ϵĶ��㣬���ı���PABQ���ܳ���Сֵʱ��PQ����ֱ�ߵĽ���ʽ��y=x+2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
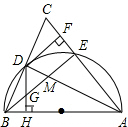 ��ͼ���ڡ�ABC�У�AB=AC����ABΪֱ���İ�ԲO��BC�ڵ�D����AC�ڵ�E������AD��BE���ڵ�M������D��DH��AB�ڵ�H����BE�ڵ�G�������н��ۣ���BD=CD����DF�ǡ�O�����ߣ��ۡ�DAC=��BDH����BM=2DG�����У������ĸ���Ϊ��������
��ͼ���ڡ�ABC�У�AB=AC����ABΪֱ���İ�ԲO��BC�ڵ�D����AC�ڵ�E������AD��BE���ڵ�M������D��DH��AB�ڵ�H����BE�ڵ�G�������н��ۣ���BD=CD����DF�ǡ�O�����ߣ��ۡ�DAC=��BDH����BM=2DG�����У������ĸ���Ϊ��������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
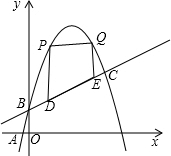 ��ͼ����֪һ�κ���y=$\frac{1}{2}$x+m����κ���y=-x2+ax+b��ͼ���ཻ�ڵ�B��0��1���͵�C������������x���һ��������A��2-$\sqrt{5}$��0����
��ͼ����֪һ�κ���y=$\frac{1}{2}$x+m����κ���y=-x2+ax+b��ͼ���ཻ�ڵ�B��0��1���͵�C������������x���һ��������A��2-$\sqrt{5}$��0�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com