
【题目】已知二次函数y=a(x+2)2+3(a<0)的图象如图所示,则以下结论:①当x>﹣2时,y随x的增大而增大;②不论a为任何负数,该二次函数的最大值总是3;③当a=﹣1时,抛物线必过原点;④该抛物线和x轴总有两个公共点.其中正确结论是( )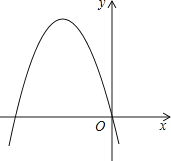
A.①②
B.②③
C.②④
D.①④
【答案】C
【解析】解:根据解析式可以得到函数的顶点坐标是(﹣2,3),对称轴是直线x=﹣2,
则当x>﹣2时,y随x的增大而减小,故①错误;
顶点坐标是(﹣2,3),开口向下,则函数的最大值是3,则②正确;
当a=﹣1时,函数的解析式是:y=﹣(x+2)2+3,(0,0)不满足函数的解析式,故函数不经过原点,故③错误;
顶点坐标是(﹣2,3),开口向下,则该抛物线和x轴总有两个公共点,故④正确.
故选C.
【考点精析】通过灵活运用二次函数的性质和二次函数图象以及系数a、b、c的关系,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3交y轴于点C,直线l为抛物线的对称轴,点P在第三象限且为抛物线的顶点.P到x轴的距离为 ![]() ,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B.
,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B. 
(1)求抛物线的表达式;
(2)直线y= ![]() x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y=
x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y= ![]() x+m的表达式;
x+m的表达式;
(3)若N为平面直角坐标系内的点,在直线y= ![]() x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A. 得分在70~80分之间的人数最多
B. 该班的总人数为40
C. 得分在90~100分之间的人数最少
D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC延长线交于点F.连接EF,与CD边交于点G,与对角线BD交于点H.
(1)若BF=BD=![]() ,求BE的长;
,求BE的长;
(2)若∠ADE=2∠BFE,求证:FH=HE+HD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点B、E、C、F在一条直线上,AB = DF,AC = DE,BE = CF.
求证: (1) △ABC ≌ △DFE ;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC各顶点的坐标分A(-2,-2),B(-4,-1),C(-4,-4).

(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在
△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,距小明家楼下D点20米的B处有一根废弃的电线杆AB,经测得此电线杆与水平线DB所成锐角为60°,在小明家楼顶C处测得电线杆顶端A的俯角为30°,底部点B的俯角为45°(点A、B、D、C在同一平面内).已知在以点B为圆心,10米长为半径的圆形区域外是一休闲广场,有关部门想把此电线杆水平放倒,且B点不动,为安全起见,他们想知道这根电线杆放倒后,顶端A能否落在休闲广场内?请通过计算回答.
(结果精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)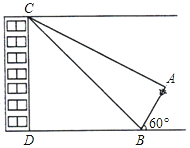
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com