
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| 3-2m |
| mx1 |
| 1-x1 |
| mx2 |
| 1-x2 |
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| -2(m-2) |
| m2-3m+3 |
1-
| ||
| 2 |
1+
| ||
| 2 |
| 1 |
| 3-2m |
| 5 |
| mx1 |
| 1-x1 |
| mx2 |
| 1-x2 |
| m(x1+x2)-2mx1x2 |
| 1-(x1+x2)+x1x2 |
| b |
| a |
| c |
| a |


科目:初中数学 来源: 题型:
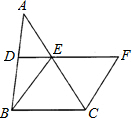 如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:
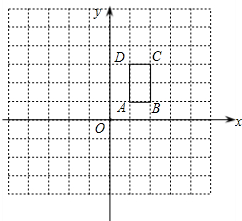 如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:
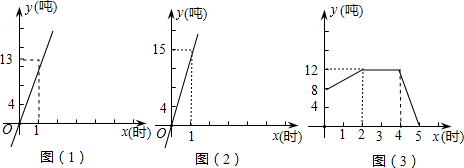
查看答案和解析>>
科目:初中数学 来源: 题型:
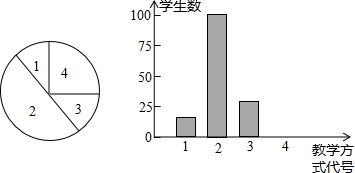
| 代号 | 教学方式 | 最喜欢人数 | 占百分比 |
| 1 | 老师讲,学生听 | 20 | 10% |
| 2 | 老师提出问题,学生探索思考 | 100 | |
| 3 | 学生自行阅读教程,独立思考 | 30 | 15% |
| 4 | 分组讨论,解决问题 | 25% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com