练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．下列长度的各组线段中，能够组成直角三角形的是（　　）
    A．8，15，17B．7，20，25C．5，11，12D．5，6，7

    分析 根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形判定则可．

    解答 解：A、82+152=172，能构成直角三角形，故正确；
    B、72+202≠252，不能构成直角三角形，故错误；
    C、52+112≠122，不能构成直角三角形，故错误；
    D、52+62≠72，不能构成直角三角形，故错误．
    故选A．

    点评 本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．在△ABC中，AB、BC、AC三边的长分别为$\sqrt{5}$，$\sqrt{10}$，$\sqrt{13}$，求这个三角形的面积．小明同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
    （1）△ABC的面积为3.5．
    （2）若△DEF的三边DE、EF、DF长分别为$\sqrt{8}$，$\sqrt{13}$，$\sqrt{17}$，请在图2的正方形网格中画出相应的△DEF，并求出△DEF的面积为5．
    （3）在△ABC中，AB=2$\sqrt{5}$，AC=4，BC=2，以AB为边向△ABC外作△ABD（D与C在AB异侧），使△ABD为等腰直角三角形，则线段CD的长为$2\sqrt{10}或2\sqrt{13}或3\sqrt{2}$．

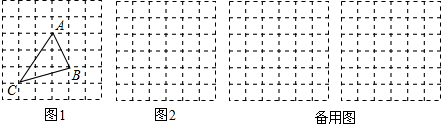
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如果$\frac{a}{b}$=2，则$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$=$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

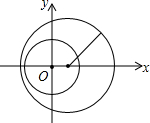    1．如图，小圆的圆心在原点，半径为3，大圆的圆心坐标为（a，0）半径为5．如果两圆内含，那么a的取值范围为（　　）
    A．-2≤a≤2B．-2＜a＜2C．0＜a＜5D．0＜a＜3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．计算：$\sqrt{（-5）^{2}}$-${（\sqrt{2}-1）}^{-1}$+${（\sqrt{2}-1）}^{0}$+|1-$\sqrt{2}$|的结果为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，直线a，b被直线c所截，下列条件中不能判定a∥b的是（　　）
    A．∠1=∠4B．∠3=∠4C．∠1=∠3D．∠2+∠3=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．阅读下列因式分解的过程，再回答所提出的问题：
    1+x+x（x+1）+x（x+1）2
    （1+x）[1+x+x（x+1）]
    =（1+x）2（1+x）
    =（1+x）3
    （1）上述分解因式的方法是提公因式法，共应用了2次．
    （2）若分解1+x+x（x+1）+x（x+1）2+x（x+1）3，则需应用上述方法3次，结果是（x+1）4．
    （3）分解因式：1+x+x（x+1）+x（x+1）2…+x（x+1）n（n为正整数）的结果是（x+1）n+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，DE∥BC，∠D=120°，∠1=∠2，求∠DEB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列式子错误的是（　　）
    A．±$\sqrt{0.04}$=±0.2B．$\sqrt{0.09}$=±0.3C．$\sqrt{（-5）^{2}}$=5D．$\root{3}{-1000}$=-10

    查看答案和解析>>

    同步练习册答案