
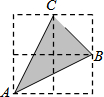
 如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于$\frac{3}{2}$,则sin∠CAB=( )
如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于$\frac{3}{2}$,则sin∠CAB=( )| A. | $\frac{3}{2}$$\sqrt{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{3}{10}$ |
分析 根据勾股定理,可得AC、AB、BC的长,根据三角形的面积公式,可得CD的长,根据正弦函数的定义,可得答案.
解答 解:如图:作CD⊥AB于D,AE⊥BC于E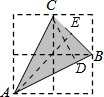 ,
,
由勾股定理,得
AB=AC=$\sqrt{5}$,BC=$\sqrt{2}$.
由等腰三角形的性质,得
BE=$\frac{1}{2}$BC=$\frac{\sqrt{2}}{2}$.
由勾股定理,得
AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\frac{3\sqrt{2}}{2}$,
由三角形的面积,得
$\frac{1}{2}$AB•CD=$\frac{1}{2}$BC•AE.
即CD=$\frac{\sqrt{2}×\frac{3\sqrt{2}}{2}}{\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$.
sin∠CAB=$\frac{CD}{AC}$=$\frac{\frac{3\sqrt{5}}{5}}{\sqrt{5}}$=$\frac{3}{5}$,
故选:B.
点评 本题考查了锐角三角函数的定义,利用了勾股定理,利用三角形的面积公式得出CD的长是解题关键.


科目:初中数学 来源: 题型:解答题
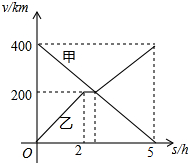 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的距离y(km)与行驶的时间为x(h)之间的函数图象如图所示.
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的距离y(km)与行驶的时间为x(h)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 所有直角三角形都相似 | |
| B. | 同弧所对的圆周角相等 | |
| C. | 平分弦的直径垂直弦且平分弦所对的弧 | |
| D. | 当b2-4ac=0时,二次函数y=ax2+bx+c的图象与坐标轴只有一个交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
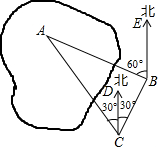 如图是某市新建的休闲人工湖,小颖同学在湖边C处测的湖中小岛A在她的北偏西30°的方向上,小颖沿北偏东30°的方向前进了40米到达B处,此时又测得湖中小岛A在她的北偏西60°的方向上,求此时小颖距湖中小岛A的距离AB.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)
如图是某市新建的休闲人工湖,小颖同学在湖边C处测的湖中小岛A在她的北偏西30°的方向上,小颖沿北偏东30°的方向前进了40米到达B处,此时又测得湖中小岛A在她的北偏西60°的方向上,求此时小颖距湖中小岛A的距离AB.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 歌手名字 | 百分比 |
| 孙楠 | 17% |
| 韩红 | a |
| 黄丽玲 | 10% |
| 李健 | 38% |
| 郑淳元 | b |
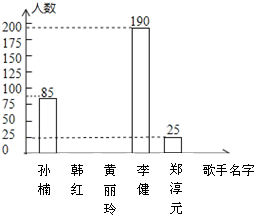
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 频数 | 频率 |
| 1 | 3 | 0.02 |
| 2 | 9 | 0.1 |
| 3 | 12 | 0.4 |
| 4 | 9 | 0.3 |
| 5 | 5.4 | 0.18 |
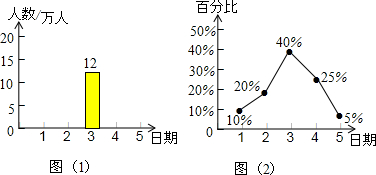
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 画图并填空:
画图并填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com