
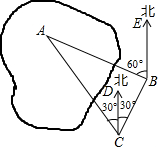
 如图是某市新建的休闲人工湖,小颖同学在湖边C处测的湖中小岛A在她的北偏西30°的方向上,小颖沿北偏东30°的方向前进了40米到达B处,此时又测得湖中小岛A在她的北偏西60°的方向上,求此时小颖距湖中小岛A的距离AB.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)
如图是某市新建的休闲人工湖,小颖同学在湖边C处测的湖中小岛A在她的北偏西30°的方向上,小颖沿北偏东30°的方向前进了40米到达B处,此时又测得湖中小岛A在她的北偏西60°的方向上,求此时小颖距湖中小岛A的距离AB.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米) 分析 先由CD∥BE,得出∠1=∠ABE=60°,根据三角形外角的性质求出∠A=∠1-∠ACD=30°,利用三角形内角和定理得到∠ABC=180°-∠A-∠ACB=90°.然后在Rt△ABC中,根据三角函数定义即可求出AB.
解答 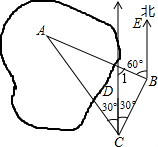 解:如图,∵CD∥BE,
解:如图,∵CD∥BE,
∴∠1=∠ABE=60°,
∴∠A=∠1-∠ACD=60°-30°=30°,
∴∠ABC=180°-∠A-∠ACB=180°-30°-60°=90°.
在Rt△ABC中,∵∠ABC=90°,∠ACB=60°,BC=40米,
∴AB=BC•tan∠ACB=40×$\sqrt{3}$≈69.3(米).
答:此时小颖距湖中小岛A的距离AB约为69.3米.
点评 本题考查了解直角三角形的应用-方向角问题,平行线的性质,三角形外角的性质,三角形内角和定理,三角函数定义,求出∠ABC=90°是解题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
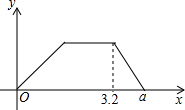 一辆货车从甲地匀速使往乙地,到达后用半个小时卸货,随即匀速返回.已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍,货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示,则a的值为( )
一辆货车从甲地匀速使往乙地,到达后用半个小时卸货,随即匀速返回.已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍,货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示,则a的值为( )| A. | 4.5 | B. | 4.9 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
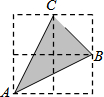 如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于$\frac{3}{2}$,则sin∠CAB=( )
如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于$\frac{3}{2}$,则sin∠CAB=( )| A. | $\frac{3}{2}$$\sqrt{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com