
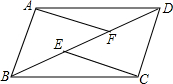
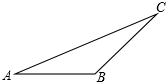
 如图所示,E,F是四边形ABCD的对角线BD上的两点,AF=CE,DF=BE,AF∥CE,求证:四边形ABCD是平行四边形.
如图所示,E,F是四边形ABCD的对角线BD上的两点,AF=CE,DF=BE,AF∥CE,求证:四边形ABCD是平行四边形. 分析 因为AE=CF,DF=BE,AF∥CE,所以可根据SAS判定△ADF≌△CBE,即有AD=BC,AD∥BC,故可根据一组对边平行且相等的四边形是平行四边形进行判定.
解答  证明:∵AF∥CE,
证明:∵AF∥CE,
∴∠AFE=∠CEF,∴∠DFA=∠BEC,
在△ADF和△CBE中,
∵$\left\{\begin{array}{l}{DF=BE}\\{∠DFE=∠BEF}\\{AF=EC}\end{array}\right.$,
∴△ADF≌△CBE(SAS),
∴AD=BC,
∴∠ADB=∠DBC,
∴AD∥BC,
∴四边形ABCD是平行四边形.
点评 此题主要考查平行四边形的判定以及全等三角形的判定.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.


科目:初中数学 来源: 题型:解答题
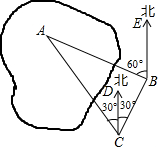 如图是某市新建的休闲人工湖,小颖同学在湖边C处测的湖中小岛A在她的北偏西30°的方向上,小颖沿北偏东30°的方向前进了40米到达B处,此时又测得湖中小岛A在她的北偏西60°的方向上,求此时小颖距湖中小岛A的距离AB.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)
如图是某市新建的休闲人工湖,小颖同学在湖边C处测的湖中小岛A在她的北偏西30°的方向上,小颖沿北偏东30°的方向前进了40米到达B处,此时又测得湖中小岛A在她的北偏西60°的方向上,求此时小颖距湖中小岛A的距离AB.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 频数 | 频率 |
| 1 | 3 | 0.02 |
| 2 | 9 | 0.1 |
| 3 | 12 | 0.4 |
| 4 | 9 | 0.3 |
| 5 | 5.4 | 0.18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
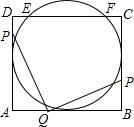 如图,已知矩形ABCD,AB=12cm,AD=10cm,⊙O与AD、AB、BC三边都相切,与DC交于点E、F.已知点P、Q、R分别从D、A、B三点同时出发,沿矩形ABCD的边逆时针方向匀速运动,点P、Q、R的运动速度分别是1cm/s、xcm/s、1.5cm/s,当点Q到达点B时停止运动,P、R两点同时停止运动,设运动时间为t(单位:s)
如图,已知矩形ABCD,AB=12cm,AD=10cm,⊙O与AD、AB、BC三边都相切,与DC交于点E、F.已知点P、Q、R分别从D、A、B三点同时出发,沿矩形ABCD的边逆时针方向匀速运动,点P、Q、R的运动速度分别是1cm/s、xcm/s、1.5cm/s,当点Q到达点B时停止运动,P、R两点同时停止运动,设运动时间为t(单位:s)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 画图并填空:
画图并填空:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com