
����Ŀ��ij��������Ӽס���������Ա��ѡȡһ����Ա�����öӲμӱ�������Ϊ�ס���������Ա������һ��ѡ������Ҫ����������Ա�����10��.�����������ݱ����ɼ���������ס���������Ա�ı����ɼ��Ƴ������µ�ͳ��ͼ(��)��
��Ա�ijɼ�ͳ�Ʊ�
�ɼ�(��λ����) | 7 | 8 | 9 | 10 |
����(�����) | 5 | 1 | 2 | 2 |
(1)��ͼ1�У�����8�����������ε�Բ�ĽǵĶ�����
(2)�����������õ��ķ����������������е�a��b��c��ֵ.
��Ա | ƽ���� | ��λ�� | ���� | ���� |
�� | 8 | 7.5 | 7 | c |
�� | a | b | 7 | 1 |
(3)���ݼס���������Ա�ijɼ���������������ѡ���Ҳμӱ���������д��һ�������ѡ���ҵ�����.

���𰸡�(1)108����(2)a=8��b=8��c=1.5��(3)�ҵķ���С˵���ҵijɼ��ȶ�.
��������
(1)��360�����Զ�Ӧ������ռ������
(2)����ƽ��������λ��������Ķ������ɵã�
(3)���Դ���λ���ͷ���ĽǶȽ�𣬴𰸲�Ψһ.
�⣺(1)��ͼ1�У���8�����������ε�Բ�ĽǵĶ���Ϊ360���![]() ��108����
��108����
(2)a��![]() ��8��
��8��
b��![]() ��8��
��8��
c��![]() ��[(7��8)2��5+(8��8)2+(9��8)2��2+(10��8)2��2]��1.5��
��[(7��8)2��5+(8��8)2+(9��8)2��2+(10��8)2��2]��1.5��
(3)�ҵķ���С˵���ҵijɼ��ȶ�(�𰸲�Ψһ).


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ٵ��ˣ�����ӭ���ֻ��г�������������ij�̳����ۼס�������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ����±���ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 4000 | 2500 |
�ۼۣ�Ԫ/���� | 4300 | 3000 |
���̳��ƻ�Ͷ��15.5��Ԫ�ʽ�ȫ�����ڹ��������ֻ����ɲ�������ȫ�����ۺ�ɻ�ë������2��Ԫ����ë����=���ۼ۩����ۣ�����������
��1�����̳�Ҫ�뾡���ܶ�Ĺ��������ֻ���Ӧ�ð��������Ľ��������������������ֻ���
��2��ͨ���г����У����̳������ڼ����ֻ��������ķ����ϣ����ټ����ֻ��Ĺ������������������ֻ��Ĺ�����������֪�����ֻ����ӵ������Ǽ����ֻ����ٵ�������2�����������ڹ����������ֻ������ʽ���16��Ԫ�����̳�����������ʹȫ�����ۺ��õ�ë�������������ë����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺����������y��ax2+bx+c��a��b��c�dz�����a��0������b2��ac����Ƹ�������Ϊ�ƽ������ߣ����磺y��2x2��2x+2�ǻƽ������ߣ�
��1������д��һ����������ͬ�Ļƽ������ߵĽ���ʽ��
��2����������y��ax2+bx+c��a��b��c�dz�����a��0���ǻƽ������ߣ���̽���ûƽ���������x��Ĺ���������������Ҫ��˵�����ɣ���
��3�����ƽ�������y��2x2��2x+2�ضԳ�������ƽ��3����λ��
��ֱ��д��ƽ�ƺ���������ߵĽ���ʽ��
�������е�����������y�ύ�ڵ�A���Գ�����x�ύ�ڵ�B������Q�ڶԳ����ϣ��������������Ƿ���ڵ�P��ʹ�Ե�P��Q��BΪ��������������AOBȫ�ȣ������ڣ�ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵����
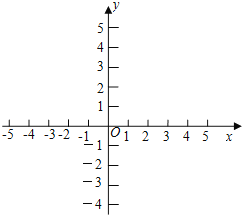
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ��ί����������Ľ��衰��ɫ�������ĺ��٣�����ij��λ����Ժ��һ�鳤30m����20m�ij����οյأ�����һ�����λ�.Ҫ���ڻ�������������ƽ�к�һ���������۵�С����ʣ��ĵط���ֲ���ݣ���ͼ��ʾ��Ҫʹ��ֲ���ݵ����Ϊ532m2����ôС�������ڵĿ���ӦΪ�����ף���ע������С�������ڵĿ�����ȣ���ÿ��С����Ϊƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y��![]() +b��a��bΪ������a��0���У���x��2ʱ��y��4����x����1ʱ��y��1����Ըú�������ͼ���������̽����
+b��a��bΪ������a��0���У���x��2ʱ��y��4����x����1ʱ��y��1����Ըú�������ͼ���������̽����
��1����ú����Ľ���ʽ����ֱ��д���ú����Ա���x��ȡֵ��Χ��
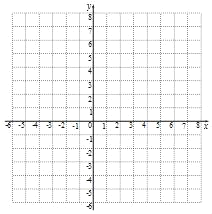
��2����������ֱ������ϵ�л����ú�����ͼ��
��3���������Ϸ�ֱ������ϵ�л�������y��2x��ͼ�������������ͼ��д������ʽ![]() +b��2x�Ľ⼯��
+b��2x�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����С��һ��Բ���ε���ˮ�ܵ����ѣ�ά����ԱΪ�����ܵ�����ȷ���ܵ�Բ�ν���İ뾶����ͼ��ˮƽ���õ����ѹܵ���ˮ���ֵĽ��森
�����㲹ȫ�����ˮ�ܵ���Բ�ν��棻
���������ˮ�ܵ���ˮ���ֵ�ˮ���AB��16cm��ˮ������ط��ĸ߶�Ϊ4cm�������Բ�ν���İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
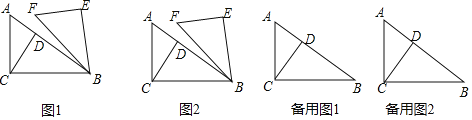
����Ŀ����ͼ1����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�D����
�ڵ�D����![]() �Ƶ�B˳ʱ����ת
�Ƶ�B˳ʱ����ת![]() �õ�
�õ�![]()
![]() ��ͼ2����
��ͼ2����![]() ʱ�����C��E֮��ľ��룻
ʱ�����C��E֮��ľ��룻
![]() ����ת�����У�����A��E��F���㹲��ʱ����AF�ij���
����ת�����У�����A��E��F���㹲��ʱ����AF�ij���
![]() ����AF����AF���е�ΪP����ֱ��д���߶�CP���ȵ���Сֵ��
����AF����AF���е�ΪP����ֱ��д���߶�CP���ȵ���Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ���Ϊֱ��![]() ��������
��������![]() ��x���ཻ��A��B���㣬����A�������Ϊ����3��0����
��x���ཻ��A��B���㣬����A�������Ϊ����3��0����

��1�����B�����ꣻ
��2����֪![]() ��CΪ��������y��Ľ��㡣
��CΪ��������y��Ľ��㡣
������P���������ϣ���![]() �����P�����ꣻ
�����P�����ꣻ
�����Q���߶�AC�ϵĶ��㣬��QD��x�ύ�������ڵ�D�����߶�QD���ȵ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��30Ԫ�����ڵ��ۼ�Ϊÿ��40Ԫ��ÿ���ڿ�����200�����г����鷴ӳ�����ÿ�����ۼ�ÿ��1Ԫ����ôÿ��������10������ÿ���Ǽ�xԪ��ÿ���ڵ�����Ϊy����
��1����y��x�ĺ�����ϵʽ��
��2����ζ��۲���ʹÿ���ڵ����������ÿ���ڵ������ϴ�ÿ���ڵ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com