
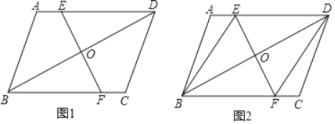
【题目】在平行四边形ABCD中,O为对角线BD的中点,EF经过点O分别交AD、BC于E、F两点,
(1)如图1,求证:AE=CF;
(2)如图2,若EF⊥BD,∠AEB=60°,请你直接写出与DE(DE除外)相等的所有线段.
【答案】(1)证明见解析;(2)BE、BF、EF、DF.
【解析】
(1)根据平行四边形的性质以及全等三角形的判定方法证明出△EOD≌△FOB,得到DE=BF,可得结论:
(2)由(1)OE=OF,而利用对角线互相垂直的平行四边形是菱形得出四边形BFDE为菱形,由∠AEB=60°可得△BEF与△BEF为等边三角形,从而得到结论.
(1)证明:![]() 四边形ABCD是平行四边形, BD为平行四边形ABCD对角线BD
四边形ABCD是平行四边形, BD为平行四边形ABCD对角线BD
![]() AD//BC,AD=BC,OB=OD.
AD//BC,AD=BC,OB=OD.
![]() ∠OED=∠OFB, ∠EDO=∠FBO.
∠OED=∠OFB, ∠EDO=∠FBO.
在△EOD与△FOB中,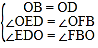 ,
,
![]() △EOD≌△FOB
△EOD≌△FOB
![]() ED=BF,
ED=BF,
又![]() AD=BC
AD=BC
![]() AE=CF.
AE=CF.
(2)由(1)得△EOD≌△FOB
![]() OE=OF,
OE=OF,
由![]() OB=OD,EF⊥BD
OB=OD,EF⊥BD
![]() 四边形BFDE为菱形,
四边形BFDE为菱形,
![]() ∠AEB=60°,
∠AEB=60°,![]() ∠BED=120°,且四边形BFDE为菱形,
∠BED=120°,且四边形BFDE为菱形,
![]() ∠BEF=∠DEF=60°,
∠BEF=∠DEF=60°, ![]() △BEF与△BEF为等边三角形,
△BEF与△BEF为等边三角形,
![]() 与DE相等的所有线段为:BE、BF、EF、DF.
与DE相等的所有线段为:BE、BF、EF、DF.


科目:初中数学 来源: 题型:
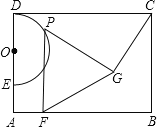
【题目】如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4![]() ,OD=2,点G在矩形内部,且∠GCB=30°,GC=2
,OD=2,点G在矩形内部,且∠GCB=30°,GC=2![]() ,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是___.
,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3为边长作等边△A3A2B3,…,则等边△A2017A2018B2018的边长是_____.
与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3为边长作等边△A3A2B3,…,则等边△A2017A2018B2018的边长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
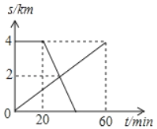
A. 8:30 B. 8:35 C. 8:40 D. 8:45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
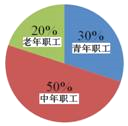
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
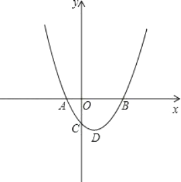
【题目】如图,抛物线y=x2﹣4x﹣1顶点为D,与x轴相交于A、B两点,与y轴相交于点C.
(1)求这条抛物线的顶点D的坐标;
(2)经过点(0,4)且与x轴平行的直线与抛物线y=x2﹣4x﹣1相交于M、N两点(M在N的左侧),以MN为直径作⊙P,过点D作⊙P的切线,切点为E,求点DE的长;
(3)上下平移(2)中的直线MN,以MN为直径的⊙P能否与x轴相切?如果能够,求出⊙P的半径;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
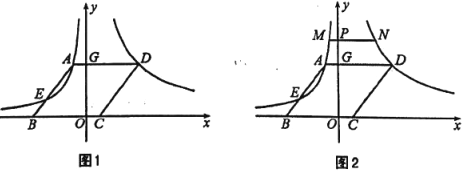
如图1,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,并与线段
,并与线段![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .已知
.已知![]() .
.
(1)求点![]() 的坐标及反比例函数
的坐标及反比例函数![]() (
(![]() )的表达式;
)的表达式;
(2)直接写出点![]() 的坐标 ;
的坐标 ;
(3)如图2,点![]() 是
是![]() 轴正半轴上的一个动点,过点
轴正半轴上的一个动点,过点![]() 作
作![]() 轴的垂线,分别交反比例函数
轴的垂线,分别交反比例函数![]() (
(![]() )与反比例函数
)与反比例函数![]() (
(![]() )的图象于点
)的图象于点![]() ,设点
,设点![]() 的坐标为
的坐标为![]()
①当![]() 时,求
时,求![]() 的值;
的值;
②在点![]() 运动过程中,是否存在某一时刻,使
运动过程中,是否存在某一时刻,使![]() ?若存在,直接写出点
?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com