
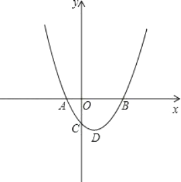
����Ŀ����ͼ��������y=x2��4x��1����ΪD����x���ཻ��A��B���㣬��y���ཻ�ڵ�C��
��1�������������ߵĶ���D�����ꣻ
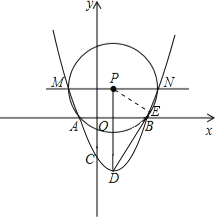
��2�������㣨0��4������x��ƽ�е�ֱ����������y=x2��4x��1�ཻ��M��N���㣨M��N����ࣩ����MNΪֱ������P������D����P�����ߣ��е�ΪE�����DE�ij���
��3������ƽ�ƣ�2���е�ֱ��MN����MNΪֱ���ġ�P�ܷ���x�����У�����ܹ��������P�İ뾶��������ܣ���˵�����ɣ�
���𰸡���1����D������Ϊ��2��-5������2��DE=6![]() ����3���ܹ����У����ɼ�����.
����3���ܹ����У����ɼ�����.
��������
��1�������䷽�����ɽ���������ʽ����Ϊ��y=��x-2��2-5���ɶ���ʽ����������������ߵĶ���D�����ꣻ
��2���ɾ����㣨0��4������x��ƽ�е�ֱ����������y=x2-4x-1�ཻ��M��N���㣨M��N����ࣩ���������M��N�����꣬�������P�����꣬Ȼ�����PE��PD�ij����������ߵ����ʣ��ɹ��ɶ����������DE�ij���
��3��������֪���ɵõ�P�ĺ�����Ϊ2��������MNΪֱ���ġ�P��x�����У��ɵ������߹��㣨2+r��r����2+r��-r�������������������ʽ�������r��ֵ�����֤����MNΪֱ���ġ�P����x�����У�
��1����y=x2-4x-1=x2-4x+4-5=��x-2��2-5��
���D��������2��-5����
��2���ߵ�y=4ʱ��x2-4x-1=4��
���x=-1��x=5��
��M������-1��4������N������5��4����
��MN=6��P�İ뾶Ϊ3����P������Ϊ��2��4����
����PE����PE��DE��
��PD=9��PE=3��
���ݹ��ɶ�����DE=6![]() ��
��
��3���ܹ����У�
���ɣ����P�İ뾶Ϊr�����������ߵĶԳ��ԣ������߹��㣨2+r��r����2+r��-r����
���������߽���ʽ�ã���2+r��2-4��2+r��-1=r��
���r=![]() ��r=
��r=![]() ����ȥ����
����ȥ����
�ѣ�2+r��-r�����������ߵã���2+r��2-4��2+r��-1=-r��
��ã�r=![]() ����r=
����r=![]() ����ȥ����
����ȥ����


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ��������ֽƬ����A=30���������۵���ʹ��C����б���ϵĵ�C�����ۺ�ΪBD����ͼ�ڣ��ٽ�����DE�۵���ʹ��A����DC�����ӳ����ϵĵ�A��������ͼ�ۣ����ۺ�DE�ij���![]() cm����BC�ij��ǣ�������
cm����BC�ij��ǣ�������
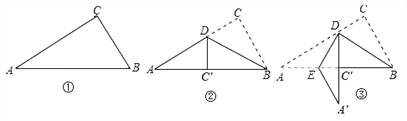
A. 3cm B. 4cm C. 5cm D. 6cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
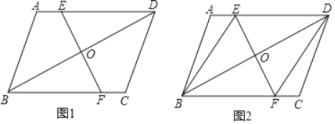
����Ŀ����ƽ���ı���ABCD�У�OΪ�Խ���BD���е㣬EF������O�ֱ�AD��BC��E��F���㣬
��1����ͼ1����֤��AE��CF��
��2����ͼ2����EF��BD����AEB��60�㣬����ֱ��д����DE��DE���⣩��ȵ������߶Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���A��x1��y1����B��x2��y2������x1x2+y1y2��0����A��B����Ϊԭ�㣬���A��B��Ϊ�����㣮���磺A��1��1����B��2����2��������1��2+1������2����0����ôA��B��Ϊ�����㣮
��1����P��Q��Ϊ�����㣬P������Ϊ����2��3����
�����Q������Ϊ��6��m������ôm��ֵΪ���٣�
�����Q������Ϊ��x��y������y��x֮��Ĺ�ϵʽ��
��2����M��N��Ϊ�����㣬ֱ��д����MON�Ķ�����
��3����C��D���ԣ�0��2��ΪԲ�ģ��뾶Ϊ2��Բ�ϵ������㣬���߶�CDΪ�ߣ�����������CDEF��Բ��F��������CDEF���ⲿ�����߶�OE���ȵ�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���![]() ��
��
![]() ��֤���÷��̱�������ʵ������
��֤���÷��̱�������ʵ������
![]() �跽�̵�����ʵ�����ֱ���
�跽�̵�����ʵ�����ֱ���![]() ��
��![]() ����
����![]() �ǹ���x�ĺ�������
�ǹ���x�ĺ�������![]() ������
������![]() ������������Ľ���ʽ��
������������Ľ���ʽ��
![]() ��
��![]() ������һԪ���η���ֻ������������k��С��0������
������һԪ���η���ֻ������������k��С��0������![]() ��Ϻ�����ͼ��ش𣺵��Ա���x����ʲô����ʱ��
��Ϻ�����ͼ��ش𣺵��Ա���x����ʲô����ʱ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
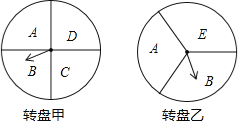
����Ŀ��ij�����ڶ�����ڼ俪չ�Żݻ���������߿���ͨ��ת��ת�̵ķ�ʽ�����ۿ��Żݣ����λ�������ַ�ʽ����ʽһ��ת��ת�̼ף�ָ��ָ��A����ʱ����������Ʒ����9���Żݡ�ָ��ָ�������������Żݣ���ʽ����ͬʱת��ת�̼�ת���ң�������ת�̵�ָ��ָ��ÿ���������ĸ��ͬ����������Ʒ����8���Żݣ�����������Żݣ���ÿ��ת���У�ָ��ָ��ÿ�����ǵĿ�������ͬ����ָ��ָ��ֽ��ߣ�������ת��ת�̣�
��1�����˿�ѡ��ʽһ��������9���Żݵĸ���Ϊ������
��2�����˿�ѡ��ʽ����������״ͼ���б����г����п��ܣ�����˿�����8���Żݵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90��,AB=5,AC=3,��D��BC��һ���㣬����AD������ACD��AD�۵�����C���ڵ�C'��������C'D��AB�ڵ�E������BC'������BC'D��ֱ��������ʱ��DE�ij�Ϊ_________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
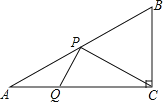
����Ŀ����Rt��ABC�У���BAC=30����б��AB=2![]() ������P��AB���ϣ�����Q��AC���ϣ��ҡ�CPQ=90�������߶�CQ������Сֵ=__________ .
������P��AB���ϣ�����Q��AC���ϣ��ҡ�CPQ=90�������߶�CQ������Сֵ=__________ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���������У���һ�ߵ��е㵽�����ߵĸ��ߵľ�����������ߵ��д��࣮
������ͼ�٣�����ABC�У�DΪ��BC���е㣬AE��BC��E�����߶�DE�ij�������BC���д��࣮
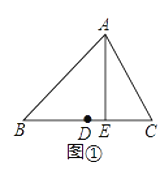
��1����������һ�ߵ��д���Ϊd��d��0������d=0����������������һ����________���ƶϵ���ѧ������________��
��2����ͼ�ڣ�����ABC�У���B=45����AB=![]() ��BC=8��ADΪ��BC�����ߣ����BC���д��࣮
��BC=8��ADΪ��BC�����ߣ����BC���д��࣮

��3����ͼ�ۣ��ھ���ABCD�У�AB=6��AD=4����EΪ��CD���е㣬����AE���ӳ���BC���ӳ����ڵ�F������AC������ACF�б�AF���д��࣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com