
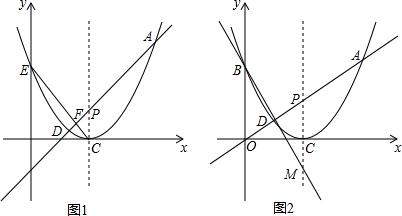
分析 (1)将两函数解析式联立即可组成方程组,解方程组即可;
(2)设D(t,$\frac{1}{2}$t2-3t+$\frac{9}{2}$),N(t,-$\frac{3}{2}$t+$\frac{9}{2}$),得出ND=-$\frac{1}{2}$t2+$\frac{3}{2}$t=-$\frac{1}{2}$(t-$\frac{3}{2}$)2+$\frac{9}{8}$,即可求出最大值;
(3)设点A、D的坐标分别为A(x1,y1)、D(x2,y2),设P、M的坐标分别为P(3,n),M(3,m),连接AB交PC于点H,过点D作DG∥x轴交PC于点G,如图2,则DG∥AB∥x轴,得到方程②③④,将②、③、④代入①中,得m=-3k即可.
解答 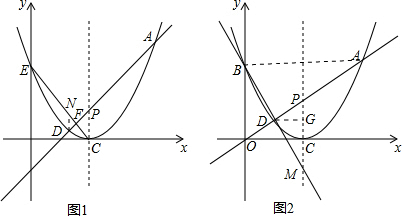 解:(1)当k=2,b=-3$\frac{1}{2}$时,直线方程化为y=2x-3$\frac{1}{2}$,
解:(1)当k=2,b=-3$\frac{1}{2}$时,直线方程化为y=2x-3$\frac{1}{2}$,
联立两方程可得$\left\{\begin{array}{l}y=\frac{1}{2}{x}^{2}-3x+\frac{9}{2}\\ y=2x-\frac{7}{2}\end{array}\right.$,
解得$\left\{\begin{array}{l}x=8\\ y=\frac{25}{2}\end{array}\right.$,$\left\{\begin{array}{l}x=2\\ y=\frac{1}{2}\end{array}\right.$;
可知,A(8,$\frac{25}{2}$),D(2,$\frac{1}{2}$).
(2)∵y=$\frac{1}{2}$(x-3)2,
∴点P的横坐标为3,
当x=3,b=2-3k时,y=2,
∴点P的坐标为(3,2),
∵CE的解析式为y=-$\frac{3}{2}$x+$\frac{9}{2}$,
过点D作DN∥PC交CE于点N,如图1,
∴$\frac{PF}{DF}$=$\frac{PC}{ND}$=$\frac{2}{ND}$,
设D(t,$\frac{1}{2}$t2-3t+$\frac{9}{2}$),N(t,-$\frac{3}{2}$t+$\frac{9}{2}$),
∴ND=-$\frac{1}{2}$t2+$\frac{3}{2}$t=-$\frac{1}{2}$(t-$\frac{3}{2}$)2+$\frac{9}{8}$,
当t=$\frac{3}{2}$时,ND的最大值为$\frac{9}{8}$.
∴$\frac{PF}{DF}$的最小值为$\frac{16}{9}$.
(3)设点A、D的坐标分别为A(x1,y1)、D(x2,y2),设P、M的坐标分别为P(3,n),
M(3,m),
∵点A、D在直线y=kx与抛物线的交点,
∴kx1=$\frac{1}{2}$x12-3x1+$\frac{9}{2}$,kx2=$\frac{1}{2}$x22-3x2+$\frac{9}{2}$,
∴x1、x2是方程$\frac{1}{2}$x2-3x+$\frac{9}{2}$=0的两根.
∴x1+x2=6+2k,x1x2=9,
连接AB交PC于点H,过点D作DG∥x轴交PC于点G,如图2,
则DG∥AB∥x轴,
∴$\frac{DG}{BH}$=$\frac{MG}{MH}$,$\frac{DG}{AH}$=$\frac{PG}{PH}$,
∵BH=AH,
∴$\frac{MG}{MH}$=$\frac{PG}{PH}$,
即$\frac{{y}_{2}-m}{{y}_{1}-m}$=$\frac{n-{y}_{2}}{{y}_{1}-n}$,
∴(y2-m)(y1-n)=(y1-m)(n-y2),
整理得2y1y2+2mn=(y1+y2)(m+n)①,
∵x1+x2=6+2k,x1x2=9,
∴y1y2=k2x1x2=9k2②,y1+y2=6k+2k2③,
∵点P(3,n)在直线y=kx上,
∴n=3k④,
将②、③、④代入①中,得m=-3k,
∵定点C的坐标为(3,0),
∴PC=MC.
点评 本题考查了二次函数综合题,(1)要根据解析式组成的方程组的解是交点坐标解答;(2)要转化为二次函数最值问题解答;(3)根据平行线分线段成比例定理等知识解答,难度较大.


科目:初中数学 来源: 题型:选择题
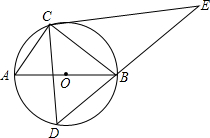 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | 5 | B. | 8 | C. | $\frac{32}{5}$ | D. | $\frac{20}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
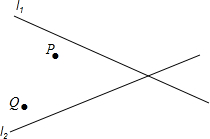 如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).
如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
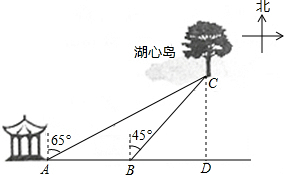 如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).
如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com