
【题目】已知:如图1,点D是△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.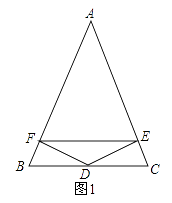
(1)求证:AE=AF;
(2)如图2,若∠BAC=60°,△ABD的面积为4,连接AD交EF于M,连接BM、CM,在不添加任何辅助线的情况下,请直接写出图中所有面积为1的三角形.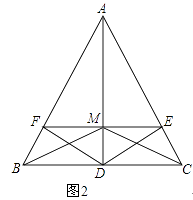
【答案】
(1)
证明:∵DE⊥AC,DF⊥AB,
∴∠DFB=∠DEC=90°,
在RT△DBF和RT△DCE中,
![]() ,
,
∴△DBF≌△DCE,
∴∠B=∠C,
∴AB=AC,∵BF=CE,
∴AF=AE.
(2)
解:∵AF=AE,
∠AFE=∠AEF,
∵∠A+2∠AFE=180°,∠A+2∠B=180°,
∴∠AFE=∠B,
∴EF∥BC,
∵BD=DC,
∴S△BDF=S△BDM=S△CDM=S△CDE,
设BD=a,∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形,
∴∠ABC=60°,AD= ![]() BD=
BD= ![]() a,
a,
∴S△ABD= ![]() a
a ![]() a=4,
a=4,
∴a2= ![]()
∴S△BDF= ![]() BFDF=
BFDF= ![]()
![]() a
a ![]() a=
a= ![]() a2=1,
a2=1,
∴S△BDF=S△BDM=S△CDM=S△CDE=1
【解析】(1)由△DBF≌△DCE得∠B=∠C,根据等角对等边得AB=AC,由此即可证明.(2)首先证明EF∥BC,得S△BDF=S△BDM=S△CDM=S△CDE , 设BD=a,根据S△ABD=4得出a2= ![]() ,再求出S△BDF=1,由此即可解决问题.
,再求出S△BDF=1,由此即可解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
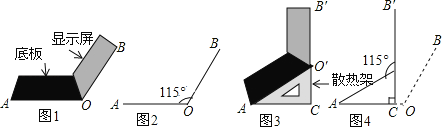
【题目】将笔记本电脑放置在水平桌面上,显示屏OB与底板OA夹角为115°(如图1),侧面示意图为图2;使用时为了散热,在底板下面垫入散热架O′AC后,电脑转到AO′B′的位置(如图3),侧面示意图为图4,已知OA=0B=20cm,B′O′⊥OA,垂足为C.
(1)求点O′的高度O′C;(精确到0.1cm)
(2)显示屏的顶部B′比原来升高了多少?(精确到0.1cm)
(3)如图4,要使显示屏O′B′与原来的位置OB平行,显示屏O′B′应绕点O′按顺时针方向旋转多少度?
参考数据:(sin65°=0.906,cos65°=0.423,tan65°=2.146.cot65°=0.446)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点为C(1,﹣2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(1)求直线AB的解析式.
(2)设点P的横坐标为x,求点E的坐标(用含x的代数式表示).
(3)求△ABE面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
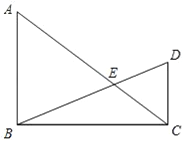
【题目】已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC=![]() ,tan∠DBC=
,tan∠DBC=![]() .
.
求:(1)边CD的长;
(2)△BCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com