
【题目】定义新运算:对于任意有理数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5,则(﹣3)⊕4的值为 .
 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,D、E分别是AC、AB的中点,且BD,CE相交于O点,某一位同学分析这个图形后得出以下结论: ①△BCD≌△CBE; ②△BDA≌△CEA; ③△BOE≌△COD; ④△BAD≌△BCD;⑤△ACE≌△BCE,上述结论一定正确的是( )
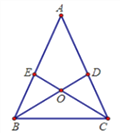
A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据宁波市统计局年报,去年我市人均生产总值为104485元,104485元用科学记数法表示为( )
A.1.04485×106元
B.0.104485×106元
C.1.04485×105元
D.10.4485×104元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(![]() 2,3),B(5,0),C(
2,3),B(5,0),C(![]() ,
, ![]() 2).
2).
①当![]() 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(![]() ,
, ![]() ),其中点E是函数
),其中点E是函数![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像如图,顶点坐标D为(3,
的图像如图,顶点坐标D为(3, ![]() )。它与
)。它与![]() 轴交于A,B两点(点A在B的左侧),与
轴交于A,B两点(点A在B的左侧),与![]() 轴交于C点,且AB的长为12. 动点P从A点出发,沿AB方向以1个单位长度/秒的速度向点B运动,设运动时间为t秒.
轴交于C点,且AB的长为12. 动点P从A点出发,沿AB方向以1个单位长度/秒的速度向点B运动,设运动时间为t秒.
(1)求二次函数的解析式;
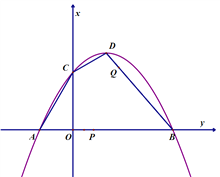
(2)当△PDB为等腰三角形时,求t的值;
(3)若动点Q与P同时从A点出发,点Q沿折线ACCDDB运动,在AC,CD,DB上运动的速度分别为3,![]() ,2 (个单位长度/秒)﹒当P,Q中的一点到达B点时,两点同时停止运动.连结PQ.
,2 (个单位长度/秒)﹒当P,Q中的一点到达B点时,两点同时停止运动.连结PQ.
①当PQ的中点恰好落在y轴上时,求t的值;
②在P,Q的运动过程中,若线段PQ的垂直平分线与线段BD有交点时,请直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com