练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】七年级派出12名同学参加数学竞赛，老师以75分为基准，把分数超过75分的部分记为正数，不足部分记为负数。评分记录如下：+15，+20，5，4，3，+4，+6，+2，+3，+5，+7，8.

    (1)这12名同学中最高分和最低分各是多少?

    (2)这些同学的平均成绩是多少?

    【答案】（1）95分，67分；（2）78.5分

    【解析】

    （1）这12名学生的评分记录中最大的数和最小的数分别与75相加，所得的和就是最高分和最低分；

    （2）求出12个评分记录的平均值再加上75所得即是这12名同学的平均成绩.

    解：（1）观察评分记录可知：其中最大的数是+20，最小的是-8，

    ∴这12名同学中最高分为：75+20=95（分）；

    最低分为：75+（-8）=67（分）.

    即这12名同学中竞赛得分最高分为95分，最低分为67分；

    （2）由题意可得这12名同学这次竞赛的平均成绩为：

    =

    =.

    ∴这12同学的平均成绩为78.5分.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

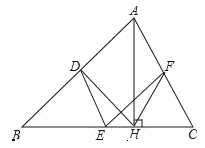
    【题目】如图，在△ABC中，点D、E、F分别是边AB、BC、CA的中点，AH是边BC上的高．

    （1）求证：四边形ADEF是平行四边形；

    （2）若∠AHF＝20°，∠AHD＝50°，求∠DEF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学生小明、小华为了解本校八年级学生每周上网的时间，各自进行了抽样调查．小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间，算得这些学生平均每周上网时间为2.5h；小华从全体320名八年级学生名单中随机抽取了40名学生，调查了他们每周上网的时间，算得这些学生平均每周上网时间为1.2h．小明与小华整理各自样本数据，如表所示．

    时间段（h/周）

    小明抽样人数

    小华抽样人数

    0～1

    6

    22

    1～2

    10

    10

    2～3

    16

    6

    3～4

    8

    2

    （每组可含最低值，不含最高值）

    请根据上述信息，回答下列问题：

    （1）你认为哪位学生抽取的样本具有代表性？_____．

    估计该校全体八年级学生平均每周上网时间为_____h；

    （2）在具有代表性的样本中，中位数所在的时间段是_____h/周；

    （3）专家建议每周上网2h以上（含2h）的同学应适当减少上网的时间，根据具有代表性的样本估计，该校全体八年级学生中有多少名学生应适当减少上网的时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

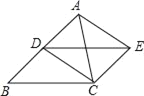
    【题目】 已知，如图，点D是△ABC的边AB的中点，四边形BCED是平行四边形．

    （1）求证：四边形ADCE是平行四边形；

    （2）在△ABC中，若AC＝BC，则四边形ADCE是　 　；（只写结论，不需证明）

    （3）在（2）的条件下，当AC⊥BC时，求证：四边形ADCE是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，并解决后面的问题．

    材料：对数的创始人是苏格兰数学家纳皮尔（J．Npler，1550-1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evler，1707-1783）才发现指数与对数之间的联系．我们知道，n个相同的因数a相乘记为，如，此时，3叫做以2为底8的对数，记为，即．

    一般地，若（且，），则n叫做以a为底b的对数，记为，即．如，则4叫做以3为底81的对数，记为，即．

    （1）计算下列各对数的值：________，________，________；

    （2）通过观察（1）中三数、、之间满足的关系式是________；

    （3）拓展延伸；下面这个一般性的结论成立吗？我们来证明

    （且，，）

    证明：设，，

    由对数的定义得：，，

    ∴，

    ∴，

    又∵，，

    ∴（且，，）.

    （4）仿照（3）的证明，你能证明下面的一般性结论吗？

    （且，，）.

    （5）计算：的值为________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙三个教师承担本学期期末考试的第17题的网上阅卷任务，若由这三人中的某一人独立完成阅卷任务，则甲需要15小时，乙需要10小时，丙需要8小时。

    （1）如果甲、乙、丙三人同时改卷，那么需要多少时间完成？

    （2）如果按照甲、乙、丙、甲、乙、丙、……的次序轮流阅卷，每一轮中每人各阅卷1小时。那么要多少小时完成？

    （3）能否把（2）题所说的甲、乙、丙的次序作适当调整，其余的不变，使得完成这项任务的时间至少提前半小时？（答题要求：如认为不能，需要说明理由；如认为能，请至少说出一种轮流的次序，并求出相应能提前多少时间完成阅卷任务）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，D，E是△ABC中AB，BC边上的点，且DE∥AC，∠ACB角平分线和它的外角的平分线分别交DE于点G和H．则下列结论错误的是( )

    A. 若BG∥CH，则四边形BHCG为矩形

    B. 若BE＝CE时，四边形BHCG为矩形

    C. 若HE＝CE，则四边形BHCG为平行四边形

    D. 若CH＝3，CG＝4，则CE＝2.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列单项式：，，，，……按此规律写出第13个单项式是____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，BN=PC．其中正确的个数是（　　）

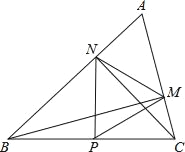
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    同步练习册答案