
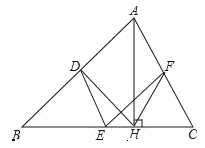
【题目】如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)若∠AHF=20°,∠AHD=50°,求∠DEF的度数.
【答案】(1)见解析;(2)70°.
【解析】
(1)结合中位线的性质证明即可;(2)先根据平行四边形的性质得到∠DEF=∠BAC,再根据题意证明∠DHF=∠BAC,得到∠DEF=∠DHF,计算∠DHF大小即可.
(1)∵D,E,F分别是边AB、BC、CA的中点,
∴DE,EF是△ABC的中位线,
∴DE∥AF,EF∥AD,
∴四边形ADEF是平行四边形.
(2)∵四边形ADEF是平行四边形,
∴∠DEF=∠BAC,
∵D,F分别是AB,CA的中点,AH是边BC上的高,
∴DH=AD,FH=AF,
∴∠DAH=∠DHA,∠FAH=∠FHA,
∵∠DAH+∠FAH=∠BAC,
∠DHA+∠FHA=∠DHF,
∴∠DHF=∠BAC,
∴∠DEF=∠DHF=∠AHF+∠AHD=70°.


科目:初中数学 来源: 题型:
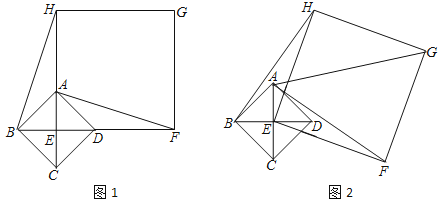
【题目】如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.
(1)如图1,点A、D分别在EH和EF上,连接BH、AF,BH和AF有何数量关系,并说明理由;
(2)将正方形EFGH绕点E顺时针方向旋转,如图2,判断BH和AF的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,点
,点![]() 是直线
是直线![]() 、
、![]() 之间的一点,连接
之间的一点,连接![]() 、
、![]() .
.
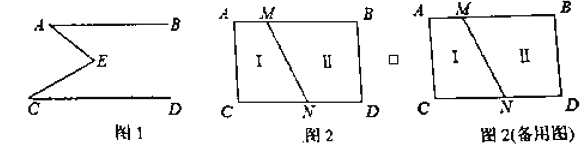
(1)问题发现:
①若![]() ,
,![]() ,则
,则![]() ___________.
___________.
②猜想图1中![]() 、
、![]() 、
、![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
(2)拓展应用:
如图2,![]() ,线段
,线段![]() 把
把![]() 这个封闭区域分为Ⅰ、Ⅱ两部分(不含边界),点
这个封闭区域分为Ⅰ、Ⅱ两部分(不含边界),点![]() 是位于这两个区域内的任意一点,请直接写出
是位于这两个区域内的任意一点,请直接写出![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
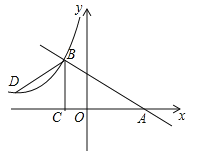
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△ADE都是直角三角形,∠C=∠AED=![]() ,点E在AB上,∠D=
,点E在AB上,∠D=![]() .如果△ABC经顺时针旋转后能与△ADE重合,那么旋转中心是点______,旋转了______度
.如果△ABC经顺时针旋转后能与△ADE重合,那么旋转中心是点______,旋转了______度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的面积;
的面积;
(2)点![]() 在
在![]() 轴上,若
轴上,若![]() 是以
是以![]() 为腰的等腰三角形,直接写出点
为腰的等腰三角形,直接写出点![]() 的坐标;
的坐标;
(3)点![]() 在
在![]() 轴上,若点
轴上,若点![]() 是直线
是直线![]() 上的一个动点,当
上的一个动点,当![]() 的面积与
的面积与![]() 的面积相等时,求点
的面积相等时,求点![]() 的坐标.
的坐标.
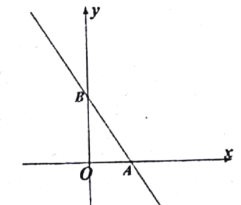
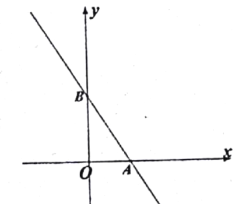
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4.5>=5,<-1.5>=-1.解决下列问题.
(1)[-4.5]=_____;<3.5>=________;
(2)若[x]=2,则x的取值范围是________;若<y>=-1,则y的取值范围是_______.
(3)若![]() ,则x为_________.
,则x为_________.
(4)已知x、y满足方程组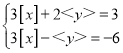
![]() ,求x、y的取值范围.
,求x、y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
问题(1):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(2):利用数轴探究:①找出满足|x﹣3|+|x+1|=6的x的所有值是 ;
②设|x﹣3|+|x+1|=p,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的值取在 的范围时,|x|+|x﹣2|的最小值是 .
问题(3):求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级派出12名同学参加数学竞赛,老师以75分为基准,把分数超过75分的部分记为正数,不足部分记为负数。评分记录如下:+15,+20,5,4,3,+4,+6,+2,+3,+5,+7,8.
(1)这12名同学中最高分和最低分各是多少?
(2)这些同学的平均成绩是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com