
【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②![]() ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=![]() PC.其中正确的个数是( )
PC.其中正确的个数是( )
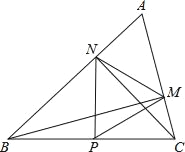
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】分析:根据直角三角形斜边上的中线等于斜边的一半可判断①正确;
先证明△ABM∽△ACN,再根据相似三角形的对应边成比例可判断②正确;
先根据直角三角形两锐角互余的性质求出∠ABM=∠ACN=30°,再根据三角形的内角和定理求出∠BCN+∠CBM=60°,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPN+∠CPM=120°,从而得到∠MPN=60°,又由①得PM=PN,根据有一个角是60°的等腰三角形是等边三角形可判断③正确;
当∠ABC=45°时,∠BCN=45°,由P为BC边的中点,得出BN=![]() PB=
PB=![]() PC,判断④正确.
PC,判断④正确.
详解:①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,∴PM=![]() BC,PN=
BC,PN=![]() BC,∴PM=PN,正确;
BC,∴PM=PN,正确;
②在△ABM与△ACN中.
∵∠A=∠A,∠AMB=∠ANC=90°,∴△ABM∽△ACN,∴![]() ,正确;
,正确;
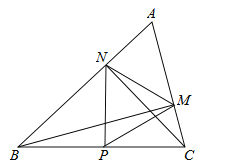
③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,∴∠ABM=∠ACN=30°.在△ABC中,∠BCN+∠CBM═180°﹣60°﹣30°×2=60°.
∵点P是BC的中点,BM⊥AC,CN⊥AB,∴PM=PN=PB=PC,∴∠BPN=2∠BCN,∠CPM=2∠CBM,∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°,∴∠MPN=60°,∴△PMN是等边三角形,正确;
④当∠ABC=45°时.
∵CN⊥AB于点N,∴∠BNC=90°,∠BCN=45°,∴BN=CN.
∵P为BC边的中点,∴PN⊥BC,△BPN为等腰直角三角形
∴BN=![]() PB=
PB=![]() PC,正确.
PC,正确.
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】七年级派出12名同学参加数学竞赛,老师以75分为基准,把分数超过75分的部分记为正数,不足部分记为负数。评分记录如下:+15,+20,5,4,3,+4,+6,+2,+3,+5,+7,8.
(1)这12名同学中最高分和最低分各是多少?
(2)这些同学的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC中,OA=2,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.
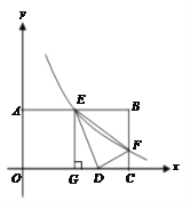
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,请证明△EGD∽△DCF,并求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=![]() .
.
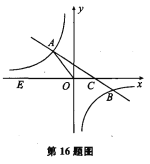
【1】求该反比例函数和一次函数的解析式
【2】求△AOC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对;
(2)如果∠AOD=50°,求∠DOP的度数.
(3)OP平分∠EOF吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图所示,小丽用棋子摆成三角形的图案,观察下面图案并填空:
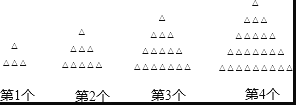
按照这样的方式摆下去,摆第5个三角形图案需要_____________枚棋子;摆第n个三角形图案需要_________枚棋子(用含有n的代数式表示);摆第99个三角形图案需要_______枚棋子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 的边长
的边长![]() .某一时刻,动点
.某一时刻,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动;同时,动点
点匀速运动;同时,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动,问:
点匀速运动,问:

(1)经过多少时间,![]() 的面积等于矩形
的面积等于矩形![]() 面积的
面积的![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=x2﹣(2m+3)x+m2+2
(1)若二次函数y的图象与x轴有两个交点,求实数m的取值范围.
(2)设二次函数y的图象与x轴的交点为A(x1,0),B(x2,0),且满足x12+x22=31+|x1x2|,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com