[题目]已知关于x的二次函数y=x2﹣x+m2+2 (1)若二次函数y的图象与x轴有两个交点.求实数m的取值范围．(2)设二次函数y的图象与x轴的交点为A(x1.0).B(x2.0).且满足x12+x22=31+|x1x2|.求实数m的值．题目和参考答案——青夏教育精英家教网—

【题目】已知关于x的二次函数y=x2﹣（2m+3）x+m2+2

（1）若二次函数y的图象与x轴有两个交点，求实数m的取值范围．

（2）设二次函数y的图象与x轴的交点为A（x1，0），B（x2，0），且满足x12+x22=31+|x1x2|，求实数m的值．

【答案】(1)m>- (2)m=2

【解析】分析：（1）利用一元二次方程根的判别式计算；

（2）利用一元二次方程根与系数的关系列出方程，解方程即可．

详解：（1）由题意得：[﹣（2m+3）]2﹣4×1×（m2+2）＞0，解得：m＞﹣；

（2）由根与系数的关系可知，x1+x2=2m+3，x1x2=m2+2，x12+x22=31+|x1x2|，（x1+x2）2﹣2x1x2=31+|x1x2|，（2m+3）2﹣2×（m2+2）=31+m2+2，整理得：m2+12m﹣28=0，解得：m1=2，m2=﹣14（舍去），当m=2时，满足x12+x22=31+|x1x2|．

练习册系列答案

小学毕业升学复习必做的18套试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，BN=PC．其中正确的个数是（　　）

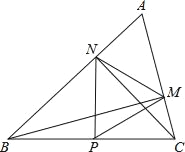
A. 1个 B. 2个 C. 3个 D. 4个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在矩形ABCD中，AB＝4，AD＝3，矩形内部有一动点P满足S矩形ABCD＝3S△PAB，则PA+PB的最小值为_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，在平面直角坐标系中，点A，B的坐标分别为A(a，0)，B(b，0)，且a，b满足|2a+6|+(2a﹣3b+12)2＝0，现同时将点A，B分别向左平移2个单位，再向上平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD．

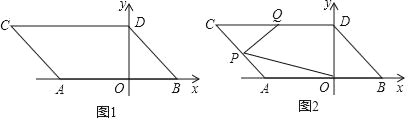
(1)请直接写出A、B、C、D四点的坐标；

(2)如图2，点P是线段AC上的一个动点，点Q是线段CD的中点，连接PQ，PO，当点P在线段AC上移动时(不与A，C重合)，请找出∠PQD，∠OPQ，∠POB的数量关系，并证明你的结论；

(3)在坐标轴上是否存在点M，使三角形MAD的面积与三角形ACD的面积相等？若存在，直接写出点M的坐标；若不存在，试说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知菱形ABCD的一个内角∠BAD=80°，对角线AC，BD相交于点O，点E在AB上，且BE=BO，则∠EOA=___________°.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】观察下列两个等式：，，给出定义如下：我们称使等式成立的一对有理数为“有趣数对”，记为如：数对，都是“有趣数对”．

（1）数对，中是“有趣数对”的是　　；

（2）若是“有趣数对”，求的值；

（3）请再写出一对符合条件的“有趣数对”　　；（注意：不能与题目中已有的“有趣数对”重复）

（4）若是“有趣数对”求的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，点是直线上的一点，将一直角三角板如图摆放，过点作射线平分.

（1）如图1，如果，依题意补全图形，求度数；

（2）当直角三角板绕点顺时针旋转一定的角度得到图2，使得直角边在直线的上方，若，其他条件不变，请你直接用含的代数式表示的度数为；

（3）当直角三角板绕点继续顺时针旋转一周，回到图1的位置，在旋转过程中你发现与之间有怎样的数量关系？请直接写出你的发现： .

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我们定义：如果两个三角形的两组对应边相等，且它们的夹角互补，我们就把其中一个三角形叫做另一个三角形的“夹补三角形”，同时把第三边的中线叫做“夹补中线．例如：图1中，△ABC与△ADE的对应边AB＝AD，AC＝AE，∠BAC+∠DAE＝180°，AF是DE边的中线，则△ADE就是△ABC的“夹补三角形”，AF叫做△ABC的“夹补中线”．

特例感知：

（1）如图2、图3中，△ABC与△ADE是一对“夹补三角形”，AF是△ABC的“夹补中线”；

①当△ABC是一个等边三角形时，AF与BC的数量关系是：　　；

②如图3当△ABC是直角三角形时，∠BAC＝90°，BC＝a时，则AF的长是　　；

猜想论证：

（2）在图1中，当△ABC为任意三角形时，猜想AF与BC的关系，并给予证明．

拓展应用：

（3）如图4，在四边形ABCD中，∠DCB＝90°，∠ADC＝150°，BC＝2AD＝6，CD＝，若△PAD是等边三角形，求证：△PCD是△PBA的“夹补三角形”，并求出它们的“夹补中线”的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为积极响应“弘扬传统文化”的号召，万州区某中学举行了一次中学生诗词大赛活动.小何同学对他所在八年级一班参加诗词大赛活动同学的成绩进行了整理，成绩分别100分、90分、80分、70分，并绘制出如下的统计图.

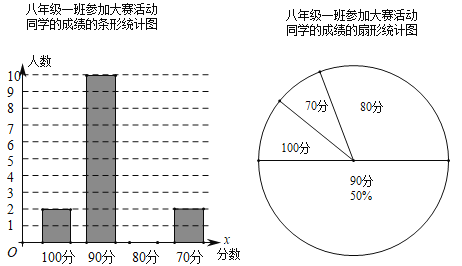
请根据以上提供的信息，解答下列问题：

（1）该校八年级（1）班参加诗词大赛成绩的众数为______分；并补全条形统计图.

（2）求该校八年级（1）班参加诗词大赛同学成绩的平均数；

（3）结合平时成绩、期中成绩和班级预选成绩（如下表），年级拟从该班小何和小王的两位同学中选一名学生参加区级决赛，按的比例计算两位同学的最终得分，请你根据计算结果确定选谁参加区级决赛.

学生姓名	平时成绩	期中成绩	预选成绩
小何	80	90	100
小王	90	100	90

查看答案和解析>>

同步练习册答案