解:(1)∵∠EDF+∠FDC=∠B+∠DEB,∠EDF=∠B,
∴∠FDC=∠DEB.
∵AB=AC,
∴∠C=∠B.
∴△CDF∽△BED.
∴

.
即

.
∴CF=8.
∴AF=AC-CF=10-8=2.
(2)分外切和内切两种情况考虑:
当⊙C和⊙A外切时,点F在线段CA上,且AF=AE,
∵AB=AC,

∴BE=CF.
∵

,
∴

.
即BE
2=BD•CD=4×8=32,
∴

.
当⊙C和⊙A内切时,点F在线段CA延长线上,且AF=AE,
∴BE=AB-AE=10-AE,CF=AC+AF=10+AE.
∵

,

,

解得

,
∴

.
∴当⊙C和⊙A相切时,BE的长为

或

.
(3)取边AC中点O,过点O分别作OG⊥DE,OQ⊥BC,垂足分别为G、Q;

过点A作AH⊥BC,垂足为H.
∵⊙O和线段DE相切,
∴

.
在Rt△CAH中,∠AHC=90°,

,
在Rt△CQO中,∠CQO=90°,
∵

,
∴

.
∴DQ=8-3=5.
∴OG=DQ.
∵OD=DO,
∴Rt△OGD≌Rt△DQO.
∴∠GOD=∠QDO.
∴OG∥BC.
∴∠EDB=∠OGD=90°.
∴

.
∴

.
∴当以边AC为直径的⊙O与线段DE相切时,

.
分析:(1)欲求AF的长可先求CF长.知道BD、,能求BE、CD,再证△BDE∽△CFD即可;
(2)(3)求BE的长关键弄清圆与圆位置关系、线与线位置关系,再运用圆心距与半径关系容易解答.
点评:此题考查相似三角形的判定和性质及圆与圆的位置关系.

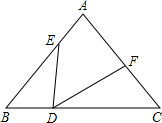 别交边AB于点E,交AC或延长线于点F.
别交边AB于点E,交AC或延长线于点F. .
. .
.
 ,
, .
. .
. ,
, ,
,
 ,
, .
. 或
或 .
.
 .
. ,
, ,
, .
. .
. .
. .
.

 学业测评一课一测系列答案
学业测评一课一测系列答案 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.