Question

5．如图，在平面直角坐标系中，一次函数y=-x+2的图象交坐标轴于点A和B，点M（a，0）在x轴正半轴上，以M为圆心，MO长为半径画⊙M．
（1）当点M在线段OA上时
①若BM平分∠OBA（如图1），求证：直线AB与⊙M相切；
②若⊙M于直线AB相交于点C、D（如图2），试用含a的代数式表示CD²；
（2）若⊙M于直线AB相交于点C、D，且∠CMD=120°，求a的值．

Answer 1

分析 （1）①首先过点M作ME⊥AB于点E，由BM平分∠OBA，根据角平分线的性质，可证得ME=MO，即可证得直线AB与⊙M相切；
②首先过点M作ME⊥AB于点E，连接MC，由一次函数y=-x+2的图象交坐标轴于点A和B，即可求得点A与B的坐标，则可得△AEM是等腰直角三角形，继而表示出ME的长，然后由垂径定理与勾股定理求得表示CD²；
（2）分别从点M在线段OA上时与点M在OA的延长线时，过点M作ME⊥CD于点E，连接MC，MD，利用含30°角的直角三角形的性质，得到方程，解方程即可求得答案．

解答 解：（1）①如图1，证明：过点M作ME⊥AB于点E，
∵∠BOM=90°，
∴MO⊥BO，
∵BM平分∠OBA，
∴ME=MO，
∴直线AB与⊙M相切；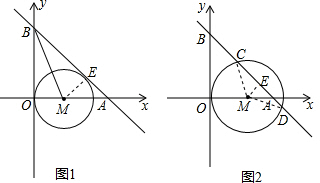

②如图2，过点M作ME⊥AB于点E，连接MC，
∵一次函数y=-x+2的图象交坐标轴于点A和B，
∴A（2，0），B（0，2），
∴∠EAM=45°，
∴ME=AE=$\frac{\sqrt{2}}{2}$AM=$\frac{\sqrt{2}}{2}$（2-a），
∵MC=OM=a，
∴CE=$\sqrt{C{M}^{2}-M{E}^{2}}$，
∵CD=2CE，
∴CD²=4CE²=4（CM²-ME²）=4[a²-$\frac{1}{2}$（2-a）²]=2a²+8a-8；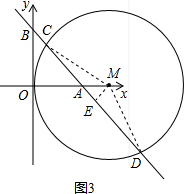

（2）如图2，点M在线段OA上时，连接MD，
∵∠CMD=120°，
∴∠MCD=∠MDC=30°，
∴MC=2ME，
∴a=2×$\frac{\sqrt{2}}{2}$（2-a），
解得：a=4-2$\sqrt{2}$；
②如图3，点M在OA的延长线时，过点M作ME⊥CD于点E，连接MC，MD，
∵△AEM是等腰直角三角形，
∴ME=AE=$\frac{\sqrt{2}}{2}$AM=$\frac{\sqrt{2}}{2}$（a-2），
∵∠CMD=120°，
∴∠MCD=∠MDC=30°，
∴MC=2ME，
∴a=2×$\frac{\sqrt{2}}{2}$（a-2），
解得：a=4+2$\sqrt{2}$；
综上，a=4-2$\sqrt{2}$或4+2$\sqrt{2}$．

点评 此题属于圆的综合题，考查了一次函数的性质、切线的判定、垂径定理、角平分线的性、勾股定理以及等腰直角三角形的性质．注意准确作出辅助线，利用分类讨论思想求解是关键．