
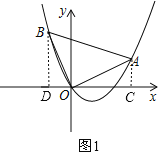
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1) B(-1.2);(2) y=![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)过A作AC⊥x轴于点C,过B作BD⊥x轴于点D,则可证明△ACO≌△ODB,则可求得OD和BD的长,可求得B点坐标;
(2)根据A、B、O三点的坐标,利用待定系数法可求得抛物线解析式;
(3)由四边形ABOP可知点P在线段AO的下方,过P作PE∥y轴交线段OA于点E,可求得直线OA解析式,设出P点坐标,则可表示出E点坐标,可表示出PE的长,进一步表示出△POA的面积,则可得到四边形ABOP的面积,再利用二次函数的性质可求得其面积最大时P点的坐标.
(1)如图1,过A作AC⊥x轴于点C,过B作BD⊥x轴于点D,
∵△AOB为等腰三角形,
∴AO=BO,
∵∠AOB=90°,
∴∠AOC+∠DOB=∠DOB+∠OBD=90°,
∴∠AOC=∠OBD,
在△ACO和△ODB中
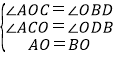
∴△ACO≌△ODB(AAS),
∵A(2,1),
∴OD=AC=1,BD=OC=2,
∴B(-1,2);
(2)∵抛物线过O点,
∴可设抛物线解析式为y=ax2+bx,
把A、B两点坐标代入可得![]() ,解得
,解得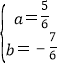 ,
,
∴经过A、B、O原点的抛物线解析式为y=![]() x2-
x2-![]() x;
x;
(3)∵四边形ABOP,
∴可知点P在线段OA的下方,
过P作PE∥y轴交AO于点E,如图2,
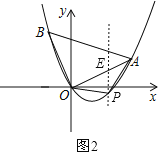
设直线AO解析式为y=kx,
∵A(2,1),
∴k=![]() ,
,
∴直线AO解析式为y=![]() x,
x,
设P点坐标为(t,![]() t2-
t2-![]() t),则E(t,
t),则E(t,![]() t),
t),
∴PE=![]() t-(
t-(![]() t2-
t2-![]() t)=-
t)=-![]() t2+
t2+![]() t=-
t=-![]() (t-1)2+
(t-1)2+![]() ,
,
∴S△AOP=![]() PE×2=PE═-
PE×2=PE═-![]() (t-1)2+
(t-1)2+![]() ,
,
由A(2,1)可求得OA=OB=![]() ,
,
∴S△AOB=![]() AOBO=
AOBO=![]() ,
,
∴S四边形ABOP=S△AOB+S△AOP=-![]() (t-1)2+
(t-1)2+![]() +
+![]() =
=![]() ,
,
∵-![]() <0,
<0,
∴当t=1时,四边形ABOP的面积最大,此时P点坐标为(1,-![]() ),
),
综上可知存在使四边形ABOP的面积最大的点P,其坐标为(1,-![]() ).
).


科目:初中数学 来源: 题型:
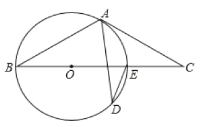
【题目】如图,BE是O的直径,点A和点D是0上的两点,过点A作⊙O的切线交BE延长线于点C.
(1)若∠ADE=25°,求∠C的度数;
(2)若AC=4,CE=2,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
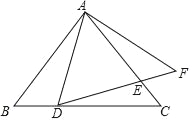
【题目】已知:如图,在△ABC中,点D、E分别在边BC、AC上,点F在DE的延长线上,AD=AF,AECE=DEEF.
(1)求证:△ADE∽△ACD;
(2)如果AEBD=EFAF,求证:AB=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
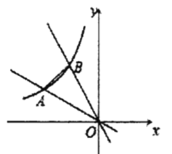
【题目】如图,函数y=![]() (x<0)的图像与直线y=-
(x<0)的图像与直线y=-![]() x交于A点,将线段OA绕O点顺时针旋转30°,交函数y=
x交于A点,将线段OA绕O点顺时针旋转30°,交函数y=![]() (x<0)的图像于B点,得到线段OB,若线段AB=3
(x<0)的图像于B点,得到线段OB,若线段AB=3![]() -
-![]() ,则k= _______________________.
,则k= _______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )

A. 13 B. 14 C. 15 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
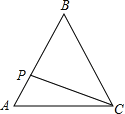
【题目】如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿![]() 的方向运动,到达点C时停止,设运动时间为x(秒),
的方向运动,到达点C时停止,设运动时间为x(秒),![]() ,则y关于x的函数的图像大致为( )
,则y关于x的函数的图像大致为( )
A. 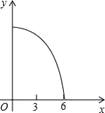 B.
B. 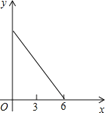 C.
C. 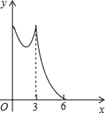 D.
D. 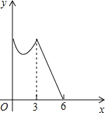
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com