练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，小明在楼上点A处测量大树的高，在A处测得大树顶部B的仰角为25°，测得大树底部C的俯角为45°．已知点A距地面的高度AD为12m，求大树的高度BC．（最后结果精确到0.1）

    【答案】解：过A作AE⊥BC于E，

    则四边形ADCE是矩形，CE=AD=12m．
    在Rt△ACE中，∵∠EAC=45°，
    ∴AE=CE=12m，
    在Rt△AEB中，∠BAE=25°，
    ∴BE=AEtan25°≈12×0.47=5.64m．
    ∴BC=BE+CE≈5.64+12≈17.6．
    答：大树的高度约为17.6m．
    【解析】过A作AE⊥BC于E，在Rt△ACE中，已知CE的长，可利用俯角∠CAE的正切函数求出AE的值；进而在Rt△ABE中，利用仰角∠BAE的正切函数求出BE的长；则BC=BE+CE．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我市某校为了创建书香校园，去年购进一批图书．经了解，科普书的单价比文学书的单价多4元，用12000元购进的科普书与用8000元购进的文学书本数相等．今年文学书和科普书的单价与去年相比保持不变，该校打算用10000元再购进一批文学书和科普书，问购进文学书550本后至多还能购进多少本科普书？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时x（h）之间的函数图象，根据图象解答以下问题：
    （1）写出A、B两地之间的距离；
    （2）求出点M的坐标，并解释该点坐标所表示的实际意义；
    （3）若两人之间保持的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是一圆形水管的截面图，已知⊙O的半径OA=13，水面宽AB=24，则水的深度CD是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当a≠0时，函数y=ax+1与函数y= 在同一坐标系中的图象可能是（　　）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的弦AB垂直半径OC于点D，∠CBA=30°，OC=3 cm，则弦AB的长为（　　）

    A.9cm
    B.3 cm
    C.
    cm
    D.
    cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），在Rt△ABC，∠ACB=90°，分别以AB、BC为一边向外作正方形ABFG、BCED，连结AD、CF，AD与CF交于点M．

    （1）求证：△ABD≌△FBC；
    （2）如图（2），已知AD=6，求四边形AFDC的面积；
    （3）在△ABC中，设BC=a，AC=b，AB=c，当∠ACB≠90°时，c2≠a2+b2 ． 在任意△ABC中，c2=a2+b2+k．就a=3，b=2的情形，探究k的取值范围（只需写出你得到的结论即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，若动点P在抛物线y=ax2上，⊙P恒过点F（0，n），且与直线y=﹣n始终保持相切，则n=（用含a的代数式表示）．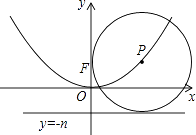

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△AOB中，∠AOB为直角，A（﹣3，a）、B（3，b），a+b﹣12=0，则△AOB的面积为_____．

    查看答案和解析>>

    同步练习册答案