
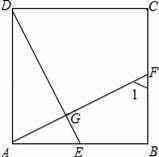
如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.
(1)观察图形,直接写出图中所有与∠1相等的角.
(2)选择图中与∠1相等的任意一个角,并加以证明.


【考点】正方形的性质;全等三角形的判定与性质.
【分析】(1)由正方形的性质得出AD∥BC,AB∥CD,∠DAE=∠ABF=90°,AD=AB,由平行线的性质得出∠DAG=∠1,∠AED=∠CDE,由HL证明Rt△ADE≌Rt△BAF,得出∠AED=∠1,即可得出∠DAG=∠AED=∠CDE=∠1;
(2)由平行线的性质即可得出∠DAG=∠1.
【解答】解:如图所示:
(1)∠DAG=∠AED=∠CDE=∠1;理由如下:
∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,∠DAE=∠ABF=90°,AD=AB,
∴∠DAG=∠1,∠AED=∠CDE,
在Rt△ADE和Rt△BAF中,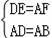
 ,
,
∴Rt△ADE≌Rt△BAF(HL),
∴∠AED=∠1,
∴∠DAG=∠AED=∠CDE=∠1;
(2)选择∠DAG=∠1;理由如下:
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAG=∠1.

【点评】本题考查了正方形的性质、平行线的性质、全等三角形的判定与性质;熟练掌握正方形的性质,证明三角形全等是解决问题的突破口.


科目:初中数学 来源: 题型:
大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )


A.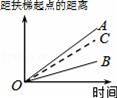
 B.
B.

C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
在劳技课上,老师请同学们在一张长为9cm,宽为8cm的长方形纸板上,剪下一个腰长为5cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边长上).请你帮助同学们画出图形并计算出剪下的等腰三角形的面积.(求出所有可能的情况)


查看答案和解析>>
科目:初中数学 来源: 题型:
某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15 C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
查看答案和解析>>
科目:初中数学 来源: 题型:
某企业为一商场提供家电配件,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 |
随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为100元,生产每件配件的人力成本为5元,其它成本3元,该配件在1至9月的销售量p1(万件)与月份x满足函数关系式p1=0.1x+1.1(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式p2=﹣0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(3)今年1月份,每件配件的原材料价格均比去年10月上涨8元,人力成本比去年增加1元,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少8a%.这样,该月完成了17万元利润的任务,请你计算出a的值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com