
ij��ҵΪһ�̳��ṩ�ҵ��������ȥ��1��9�£��������ԭ���ϼ۸�һ·������ÿ�������ԭ���ϼ۸�y1��Ԫ�����·�x��1��x��9����xȡ������֮��ĺ�����ϵ���±���
| �·�x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| �۸�y1��Ԫ/���� | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 |
���Ź��ҵ��ش�ʩ�ij�̨��ԭ���ϼ۸������������10��12��ÿ�������ԭ���ϼ۸�y2��Ԫ�����·�x��10��x��12����xȡ������֮�������ͼ��ʾ�ı仯���ƣ�
��1����۲����еı�������ѧ����һ�κ�������������������κ������й�֪ʶ��ֱ��д��y1��x֮��ĺ�����ϵʽ��������ͼ��ʾ�ı仯���ƣ�ֱ��д��y2��x֮�������һ�κ�����ϵʽ��
��2����ȥ������ÿ�����ۼ�Ϊ100Ԫ������ÿ������������ɱ�Ϊ5Ԫ�������ɱ�3Ԫ���������1��9�µ�������p1����������·�x���㺯����ϵʽp1=0.1x+1.1��1��x��9����xȡ��������10��12�µ�������p2����������·�x���㺯����ϵʽp2=��0.1x+2.9��10��x��12����xȡ����������ȥ���ĸ������۸��������������������������
��3������1�·ݣ�ÿ�������ԭ���ϼ۸����ȥ��10������8Ԫ�������ɱ���ȥ������1Ԫ�������ɱ�û�б仯������ҵ��ÿ��������ۼ���ȥ��Ļ��������a%�����ͬʱÿ������������ȥ��12�µĻ����ϼ���8a%�����������������17��Ԫ�����������������a��ֵ��


�����㡿���κ�����Ӧ�ã�
��ר�⡿�������⣮
����������1�����ݱ�����Եõ�y1��x֮��ĺ�����ϵʽ�����ݺ���ͼ����Եõ�y2��x֮���һ�κ�����ϵʽ��
��2������������Էֱ������1��x��9ʱ����������10��x��12ʱ����������ֵ��Ȼ����бȽϣ��������ȥ���ĸ������۸��������������������������
��3��������Ŀ�е���Ϣ�����г���Ӧ�Ĺ�ϵʽ���Ӷ��������a��ֵ��
����𡿽⣺��1����y1=kx+b��
�ɱ���ɵã�
 ��
��
���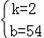
 ��
��
��y1=2x+54��1��x��9��xȡ��������
��y2=ax+b��
�ɺ���ͼ���֪���㣨10��73������12��75���ں�����ͼ���ϣ�
��

��ã�

��y2=x+63��10��x��12��xȡ��������
��y1=2x+54��1��x��9��xȡ��������y2=x+63��10��x��12��xȡ��������
��2����ȥ���x�µ�����Ϊw��Ԫ��
��1��x��9��xȥ����ʱ��
w=��100��5��3��y1����p1
=��92��2x��54����0.1x+1.1��
=��0.2x2+1.6x+41.8
=��0.2��x��4��2+45
��1��x��9��
�൱x=4ʱ��wȡ�����ֵ����ʱw=45��
��10��x��12��xȡ������
w=��100��5��3��y2��p2
=��92��x��63������0.1x+2.9��
=0.1��x��29��2��
��10��x��12��xȡ������
�൱x=10ʱ��wȡ�����ֵ����ʱw=36.1��
��45��36.1
��ȥ��4�����۸����������������������45��Ԫ��
��3��������ɵã�
[100��1+a%����81��6��3]������0.1��12+2.9����1��8a%��=17
���a1=2.5��a2=0����ȥ��
��a��ֵΪ2.5��
�����������⿼����κ�����Ӧ�á������Ľ���ʽ����������ֵ������Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ��������
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��������ABCD�У���E��F�ֱ��ڱ�AB��BC�ϣ�AF=DE��AF��DE�ཻ�ڵ�G��
��1���۲�ͼ�Σ�ֱ��д��ͼ���������1��ȵĽǣ�
��2��ѡ��ͼ�����1��ȵ�����һ���ǣ�������֤����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
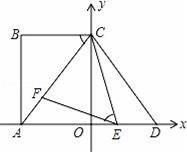
��ͼ����ƽ��ֱ������ϵ�У���A��C�ֱ���x�ᡢy���ϣ��ı���ABCOΪ���Σ�AB=16����D���A����y��Գƣ�tan��ACB=
 ����CDE=��CAO����E��F�ֱ����߶�AD��AC�ϵĶ��㣨��E�����A��D�غϣ����ҡ�CEF=��ACB��
����CDE=��CAO����E��F�ֱ����߶�AD��AC�ϵĶ��㣨��E�����A��D�غϣ����ҡ�CEF=��ACB��
��1����AC�ij��͵�D�����ꣻ
��2��֤������AEF�ס�DCE��
��3������EFCΪ����������ʱ�����E�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��һ������ε��ڽǺ���1080�ȣ����������εı���Ϊ��������
A��6 B��7 C��8 D��10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��������ABCD�У�ACΪ�Խ��ߣ�EΪAC��һ�㣬����EB��ED��
��1����֤����BEC�ա�DEC��
��2���ӳ�BE��AD��F������BED=120��ʱ�����EFD�Ķ�����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x����A����1��0����B��5��0�����㣬��y���ڵ�C����D���߶�OB��һ���㣬����CD�����߶�CD�Ƶ�D˳ʱ����ת90��õ��߶�DE������E��ֱ��l��x����H������C��CF��l��F��
��1���������߽���ʽ��
��2����ͼ2������Fǡ������������ʱ�����߶�OD�ij���
��3���ڣ�2���������£�
������DF����tan��FDE��ֵ��
����̽����ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣿�����ڣ���ֱ��д����G�����ꣻ�������ڣ���˵�����ɣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�����κ���y=ax2+bx+c��a��0����ͼ����x�����������㣬����ֱ�Ϊ��x1��0������x2��0������x1��x2��ͼ������һ��M��x0��y0����x���·����������ж���ȷ���ǣ�������
A��a��0 B��b2��4ac��0
C��x1��x0��x2 D��a��x0��x1����x0��x2����0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com