
��ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x����A����1��0����B��5��0�����㣬��y���ڵ�C����D���߶�OB��һ���㣬����CD�����߶�CD�Ƶ�D˳ʱ����ת90��õ��߶�DE������E��ֱ��l��x����H������C��CF��l��F��
��1���������߽���ʽ��
��2����ͼ2������Fǡ������������ʱ�����߶�OD�ij���
��3���ڣ�2���������£�
������DF����tan��FDE��ֵ��
����̽����ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣿�����ڣ���ֱ��д����G�����ꣻ�������ڣ���˵�����ɣ�


�����㡿���κ����ۺ��⣮
��ר�⡿ѹ���⣮
����������1�����ô���ϵ������ü��ɣ�
��2������C�����������F�����꣬Ȼ��ͨ����OCD�ա�HDE���ó�DH=OC=3���������OD�ij���
��3������ȷ��C��D��E��F�ĵ㹲Բ������Բ�ܽǶ�����á�ECF=��EDF������tan��ECF=
 =
=
 =
=
 ���������tan��FDE=
���������tan��FDE=
 ��
��
������CE���ó���CDE�ǵ���ֱ�������Σ��ó���CED=45�㣬��D����DG1��CE����ֱ��l��G1����D����DG2��CE����ֱ��l��G2�����EDG1=45�㣬��EDG2=45�㣬���ֱ��CE�Ľ���ʽΪy=��
 x+3���������ֱ��DG1�Ľ���ʽΪy=��
x+3���������ֱ��DG1�Ľ���ʽΪy=��
 x+m��ֱ��DG2�Ľ���ʽΪy=2x+n����D��������뼴�����m��n���Ӷ���ý���ʽ���������G�����꣮
x+m��ֱ��DG2�Ľ���ʽΪy=2x+n����D��������뼴�����m��n���Ӷ���ý���ʽ���������G�����꣮
����𡿽⣺��1����ͼ1����������y=ax2+bx+3��x����A����1��0����B��5��0�����㣬
��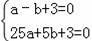
 ��
��
���
 ��
��
�������߽���ʽΪy=��
 x2+
x2+
 x+3��
x+3��
��2����ͼ2���ߵ�Fǡ�����������ϣ�C��0��3����


��F��������Ϊ3��
��y=3����y=��
 x2+
x2+
 x+3�ã�3=��
x+3�ã�3=��
 x2+
x2+
 x+3��
x+3��
���x=0��x=4��
��F��4��3��
��OH=4��
�ߡ�CDE=90�㣬
���ODC+��EDH=90�㣬
���OCD=��EDH��
�ڡ�OCD�͡�HDE�У�

 ��
��
���OCD�ա�HDE��AAS����
��DH=OC=3��
��OD=4��3=1��
��3������ͼ3������CE��

��OCD�ա�HDE��
��HE=OD=1��
��BF=OC=3��
��EF=3��1=2��
�ߡ�CDE=��CFE=90�㣬
��C��D��E��F�ĵ㹲Բ��
���ECF=��EDF��
��RT��CEF����CF=OH=4��
��tan��ECF=
 =
=
 =
=
 ��
��
��tan��FDE=
 ��
��
����ͼ4����CE��


��CD=DE����CDE=90�㣬
���CED=45�㣬
��D����DG1��CE����ֱ��l��G1����D����DG2��CE����ֱ��l��G2�����EDG1=45�㣬��EDG2=45��
��EH=1��OH=4��
��E��4��1����
��C��0��3����
��ֱ��CE�Ľ���ʽΪy=��
 x+3��
x+3��
��ֱ��DG1�Ľ���ʽΪy=��
 x+m��
x+m��
��D��1��0����
��0=��
 ��1+m�����m=
��1+m�����m=
 ��
��
��ֱ��DG1�Ľ���ʽΪy=��
 x+
x+
 ��
��
��x=4ʱ��y=��
 +
+
 =��
=��
 ��
��
��G1��4����
 ����
����
��ֱ��DG2�Ľ���ʽΪy=2x+n��
��D��1��0����
��0=2��1+n�����n=��2��
��ֱ��DG2�Ľ���ʽΪy=2x��2��
��x=4ʱ��y=2��4��2=6��
��G2��4��6����
���ϣ���ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣬��G������Ϊ��4����
 ����4��6����
����4��6����


�������������Ƕ��κ������ۺ��⣬�����˴���ϵ��������κ����Ľ���ʽ��һ�κ����Ľ���ʽ��������ȫ�ȵ��ж������ʣ�����ֱ�������ε����ʣ�ƽ���ߵ����ʵȣ����ν��˼���Ӧ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij��ҵΪһ�̳��ṩ�ҵ��������ȥ��1��9�£��������ԭ���ϼ۸�һ·������ÿ�������ԭ���ϼ۸�y1��Ԫ�����·�x��1��x��9����xȡ������֮��ĺ�����ϵ���±���
| �·�x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| �۸�y1��Ԫ/���� | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 |
���Ź��ҵ��ش�ʩ�ij�̨��ԭ���ϼ۸������������10��12��ÿ�������ԭ���ϼ۸�y2��Ԫ�����·�x��10��x��12����xȡ������֮�������ͼ��ʾ�ı仯���ƣ�
��1����۲����еı�������ѧ����һ�κ�������������������κ������й�֪ʶ��ֱ��д��y1��x֮��ĺ�����ϵʽ��������ͼ��ʾ�ı仯���ƣ�ֱ��д��y2��x֮�������һ�κ�����ϵʽ��
��2����ȥ������ÿ�����ۼ�Ϊ100Ԫ������ÿ������������ɱ�Ϊ5Ԫ�������ɱ�3Ԫ���������1��9�µ�������p1����������·�x���㺯����ϵʽp1=0.1x+1.1��1��x��9����xȡ��������10��12�µ�������p2����������·�x���㺯����ϵʽp2=��0.1x+2.9��10��x��12����xȡ����������ȥ���ĸ������۸��������������������������
��3������1�·ݣ�ÿ�������ԭ���ϼ۸����ȥ��10������8Ԫ�������ɱ���ȥ������1Ԫ�������ɱ�û�б仯������ҵ��ÿ��������ۼ���ȥ��Ļ��������a%�����ͬʱÿ������������ȥ��12�µĻ����ϼ���8a%�����������������17��Ԫ�����������������a��ֵ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
С�������г���ѧ����ʼ�������ٶ�������ʻ����������;ʱ�����г����˹��ϣ�ֻ��ͣ�����������ú����µ����ϿΣ�������ǰ�ӿ����ٶȼ���������ʻ����������ʻ·��s��m������ʱ��t��min���ĺ���ͼ����ô����С����ʻ����Ĵ���ͼ���ǣ�������
A��
 B��
B��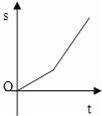

C��
 D��
D��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��߳�Ϊ2a�������ε�����A��ֱ��l�ϣ�����һ��Աߴ�ֱ��ֱ��l���뾶Ϊr�ġ�O��Բ��O��ֱ��l���˶�����A��O�����Ϊd��


��1����ͼ�٣���r��aʱ������d��a��r֮���ϵ������O�������εĹ�������������±���
| d��a��r֮���ϵ | ������ĸ��� |
| d��a+r | |
| d=a+r | |
| a��r��d��a+r | |
| d=a��r | |
| d��a��r |
���ԣ���r��aʱ����O�������εĹ�����ĸ����������� ������
��2����ͼ�ڣ���r=aʱ������d��a��r֮���ϵ������O�������εĹ�������������±���
| d��a��r֮���ϵ | ������ĸ��� |
| d��a+r | |
| d=a+r | |
| a��d��a+r | |
| d��a |
���ԣ���r=aʱ����O�������εĹ���������������� ������
��3����ͼ�ۣ�����O����������5��������ʱ����˵��r=
 a��
a��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ��ֱ������ϵxOy�У�Rt��OA1C1��Rt��OA2C2��Rt��OA3C3��Rt��OA4C4����б�߶����������ϣ���A1OC1=��A2OC2=��A3OC3=��A4OC4��=30�㣮����A1������Ϊ��3��0����OA1=OC2��OA2=OC3��OA3=OC4���������ι��ɣ���A2016��������Ϊ��������


A��0 B����3����


 ��2015 C����2
��2015 C����2
 ��2016 D��3����
��2016 D��3����


 ��2015
��2015
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪������y1=ax2+bx+c��a��0��a��c������A��1��0��������ΪB���������߲������������ޣ�
��1��ʹ��a��c��ʾb��
��2���жϵ�B�������ޣ���˵�����ɣ�
��3����ֱ��y2=2x+m������B������������߽�����һ��C��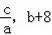
 ������x��1ʱy1��ȡֵ��Χ��
������x��1ʱy1��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��Ȼ��4��5��5��x��y��С�������к�����λ��Ϊ4�������������Ψһ��������5����ô����������������x��y�У�x+y�����ֵ�ǣ�������
A��3 B��4 C��5 D��6
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com