
若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,则下列判断正确的是( )
A.a>0 B.b2﹣4ac≥0
C.x1<x0<x2 D.a(x0﹣x1)(x0﹣x2)<0
D【考点】抛物线与x轴的交点.
【专题】压轴题.
【分析】根据抛物线与x轴有两个不同的交点,根的判别式△>0,再分a>0和a<0两种情况对C、D选项讨论即可得解.
【解答】解:A、二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点无法确定a的正负情况,故本选项错误;
B、∵x1<x2,
∴△=b2﹣4ac>0,故本选项错误;
C、若a>0,则x1<x0<x2,
若a<0,则x0<x1<x2或x1<x2<x0,故本选项错误;
D、若a>0,则x0﹣x1>0,x0﹣x2<0,
所以,(x0﹣x1)(x0﹣x2)<0,
∴a(x0﹣x1)(x0﹣x2)<0,
若a<0,则(x0﹣x1)与(x0﹣x2)同号,
∴a(x0﹣x1)(x0﹣x2)<0,
综上所述,a(x0﹣x1)(x0﹣x2)<0正确,故本选项正确.
故选:D.
【点评】本题考查了二次函数与x轴的交点问题,熟练掌握二次函数图象以及图象上点的坐标特征是解题的关键,C、D选项要注意分情况讨论.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
某企业为一商场提供家电配件,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 |
随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为100元,生产每件配件的人力成本为5元,其它成本3元,该配件在1至9月的销售量p1(万件)与月份x满足函数关系式p1=0.1x+1.1(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式p2=﹣0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(3)今年1月份,每件配件的原材料价格均比去年10月上涨8元,人力成本比去年增加1元,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少8a%.这样,该月完成了17万元利润的任务,请你计算出a的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )


A.0 B.﹣3×(


 )2015 C.(2
)2015 C.(2
 )2016 D.3×(
)2016 D.3×(


 )2015
)2015
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),顶点为B,且抛物线不经过第三象限.
(1)使用a、c表示b;
(2)判断点B所在象限,并说明理由;
(3)若直线y2=2x+m经过点B,且与该抛物线交于另一点C(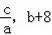
 ),求当x≥1时y1的取值范围.
),求当x≥1时y1的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是( )
A.
 B.
B.
 C.
C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
某过天桥的设计图是梯形ABCD(如图所示),桥面DC与地面AB平行,DC=62米,AB=88米.左斜面AD与地面AB的夹角为23°,右斜面BC与地面AB的夹角为30°,立柱DE⊥AB于E,立柱CF⊥AB于F,求桥面DC与地面AB之间的距离(精确到0.1米)sin23°=0.3907,cos23°=0.9205,tan23°=0.4245


查看答案和解析>>
科目:初中数学 来源: 题型:
自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么,所有满足条件的x,y中,x+y的最大值是( )
A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com