
【题目】在平面直角坐标系xOy中,抛物线![]() 与
与![]() 轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.
轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.
(1)求直线BC的解析式;
(2)点D在抛物线上,且点D的横坐标为4.将抛物线在点A,D之间的部分(包含点A,D)记为图象G,若图象G向下平移![]() (
(![]() )个单位后与直线BC只有一个公共点,求
)个单位后与直线BC只有一个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
试题(1)首先根据抛物线![]() 求出与
求出与![]() 轴交于点A,顶点为点B的坐标,然后求出点A关于抛物线的对称轴对称点C的坐标,设设直线BC的解析式为
轴交于点A,顶点为点B的坐标,然后求出点A关于抛物线的对称轴对称点C的坐标,设设直线BC的解析式为![]() .代入点B,点C的坐标,然后解方程组即可;( 2)求出点D、E、F的坐标,设点A平移后的对应点为点
.代入点B,点C的坐标,然后解方程组即可;( 2)求出点D、E、F的坐标,设点A平移后的对应点为点![]() ,点D平移后的对应点为点
,点D平移后的对应点为点![]() .当图象G向下平移至点
.当图象G向下平移至点![]() 与点E重合时, 点
与点E重合时, 点![]() 在直线BC上方,此时t=1;当图象G向下平移至点
在直线BC上方,此时t=1;当图象G向下平移至点![]() 与点F重合时,点
与点F重合时,点![]() 在直线BC下方,此时t=3.从而得出
在直线BC下方,此时t=3.从而得出![]() .
.
试题解析:解:(1)∵抛物线![]() 与
与![]() 轴交于点A,
轴交于点A,
∴点A的坐标为(0,2). 1分
∵![]() ,
,
∴抛物线的对称轴为直线![]() ,顶点B的坐标为(1,
,顶点B的坐标为(1,![]() ). 2分
). 2分
又∵点C与点A关于抛物线的对称轴对称,
∴点C的坐标为(2,2),且点C在抛物线上.
设直线BC的解析式为![]() .
.
∵直线BC经过点B(1,![]() )和点C(2,2),
)和点C(2,2),
∴ 解得
解得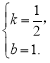
∴直线BC的解析式为
![]() . 3分
. 3分
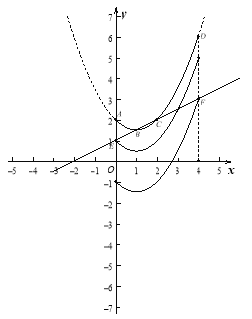
(2)∵抛物线![]() 中,
中,
当![]() 时,
时,![]() ,
,
∴点D的坐标为(4,6). 4分
∵直线![]() 中,
中,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴如图,点E的坐标为(0,1),
点F的坐标为(4,3).
设点A平移后的对应点为点![]() ,点D平移后的对应点为点
,点D平移后的对应点为点![]() .
.
当图象G向下平移至点![]() 与点E重合时, 点
与点E重合时, 点![]() 在直线BC上方,
在直线BC上方,
此时t=1; 5分
当图象G向下平移至点![]() 与点F重合时,点
与点F重合时,点![]() 在直线BC下方,此时t=3.
在直线BC下方,此时t=3.
6分
结合图象可知,符合题意的t的取值范围是![]() . 7分
. 7分


科目:初中数学 来源: 题型:
【题目】如下图,已知直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() :
:![]() 交
交![]() 于点
于点![]() .
.
(1)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)如图1,点E是线段OB的中点,连结AE,点F是射线OG上一点, 当![]() ,且
,且![]() 时,求
时,求![]() 的长;
的长;
(3)如图2,若![]() ,过
,过![]() 点作
点作![]() ∥
∥![]() ,交
,交![]() 轴于点
轴于点![]() ,此时在
,此时在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.
(1)求证:① △AEF≌△DEB;② 四边形ADCF是平行四边形;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
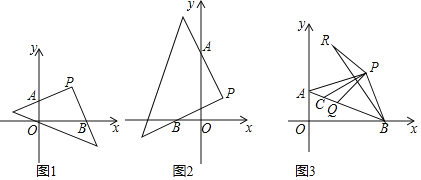
【题目】(1)已知:点P(a,b),P点坐标满足![]() +|3a﹣2b﹣4|=0将45°角的三角板,直角顶点放在P处,两边与坐标轴交于A、B两点,如图1,求a、b的值.
+|3a﹣2b﹣4|=0将45°角的三角板,直角顶点放在P处,两边与坐标轴交于A、B两点,如图1,求a、b的值.
(2)将三角板绕P点,顺时针旋转,两边与x轴交于B点,与y轴交于A点,求|OA﹣OB|的值.
(3)如图3,若Q是线段AB上一动点,C为AQ中点,PR⊥PQ且PR=PQ,连BR,请同学们判断线段BR与PC之间的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
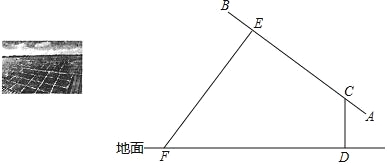
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中线段AB、CD、EF表示支撑角钢,太阳能电池板紧贴在支撑角钢AB上且长度均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD、EF与地面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,已知小正方形的边长为1,![]() 与
与![]() 的顶点均为格点,边
的顶点均为格点,边![]() ,
,![]() 交于点
交于点![]() ,下面有四个结论:①
,下面有四个结论:①![]() ;②图中阴影部分(即
;②图中阴影部分(即![]() 与
与![]() 重叠部分)的面积为1.5;③
重叠部分)的面积为1.5;③![]() 为等边三角形;④
为等边三角形;④![]() .其中结论正确的个数为( )
.其中结论正确的个数为( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李以每千克0.8元的价格从批发市场购进若干千克的西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完,销售金额与西瓜的千克数之间的关系如图所示,那么小李赚了( )
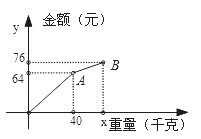
A. 32元B. 36元C. 38元D. 44元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com