
【题目】抛物线y=x2+(m﹣3)x﹣m+2的图象交x轴正半轴于点A,交x轴负半轴于点B,交y轴于点C.
(1)求m的取值范围;
(2)若△ABC恰为等腰三角形,求m.
【答案】(1)m>2(2)3+![]() ;3
;3
【解析】
(1)抛物线与x轴正半轴交于点A,交x轴负半轴于点B,则x2+(m﹣3)x﹣m+2=0的两个根一正一负;即x1x2<0,由此即可求得m的取值范围;(2)用含有m的式子表示出点ABC的坐标,在分AB=BC、AB=AC、AC=BC三种情况求m的值即可.
(1)可知x2+(m﹣3)x﹣m+2=0的两个根一正一负,
即x1x2=﹣m+2<0,
得m>2;
(2)令y=0,得x=1或﹣m+2,
∴A(1,0),B(﹣m+2,0),C(0,﹣m+2),
∵△ABC恰为等腰三角形,
∴当AB=BC时,m﹣1=![]() (m﹣2),
(m﹣2),
解得m=3+![]() ;
;
当AB=AC时,m﹣1=![]() ,
,
解得m=2(舍去);
当AC=BC时,![]() (2﹣m)=
(2﹣m)=![]() ,
,
解得m=3或1(舍去1);
∴m的值为3+![]() ;3.
;3.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
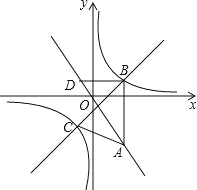
【题目】如图,在平面直角坐标系xOy中,点A(a,﹣![]() )在直线y=﹣
)在直线y=﹣![]() 上,AB∥y轴,且点B的纵坐标为1,双曲线y=
上,AB∥y轴,且点B的纵坐标为1,双曲线y=![]() 经过点B.
经过点B.
(1)求a的值及双曲线y=![]() 的解析式;
的解析式;
(2)经过点B的直线与双曲线y=![]() 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为![]() .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣![]() 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
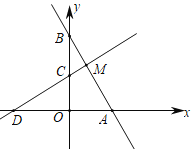
【题目】如图,直线l1:y=﹣2x+2交x轴于点A,交y轴于点B,直线l2:y=![]() x+1交x轴于点D,交y轴于点C,直线l1、l2交于点M.
x+1交x轴于点D,交y轴于点C,直线l1、l2交于点M.
(1)点M坐标为_____;
(2)若点E在y轴上,且△BME是以BM为一腰的等腰三角形,则E点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
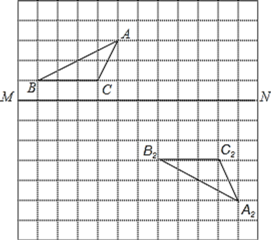
【题目】在如图所示的方格纸中.
(1)作出![]() 关于
关于![]() 对称的图形
对称的图形![]() .
.
(2)说明![]() ,可以由
,可以由![]() 经过怎样的平移变换得到?
经过怎样的平移变换得到?
(3)以![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 的中点为坐标原点,建立直角坐标系,试在
的中点为坐标原点,建立直角坐标系,试在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最小(保留找点
最小(保留找点![]() 的作图痕迹,描出点
的作图痕迹,描出点![]() 的位置,并写出点
的位置,并写出点![]() 的坐标).
的坐标).
查看答案和解析>>
科目:初中数学 来源: 题型:
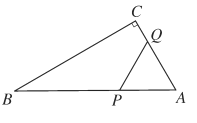
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发以
出发以![]() /
/![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() /
/![]() 的速度向点
的速度向点![]() 运动,设
运动,设![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,运动的时间为
同时出发,运动的时间为![]() .
.
(1)求![]() 、
、![]() 的长(用含
的长(用含![]() 的式子表示).
的式子表示).
(2)当![]() 为何值时,
为何值时,![]() 是以
是以![]() 为底边的等腰三角形?
为底边的等腰三角形?
(3)当![]() 为何值时,
为何值时,![]() //
//![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
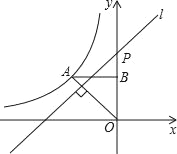
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C
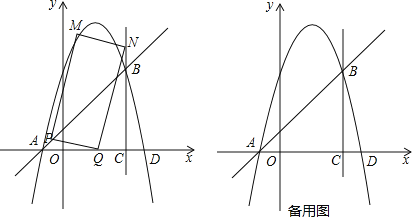
(1)求抛物线的解析式;
(2)点P从点A出发,以每秒![]() 个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.
①当t为何值时,矩形PQNM的面积最小?并求出最小面积;
②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com