
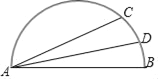
【题目】如图,在半圆O中,AB是直径,AB=13,点C是半圆O上一点,AC=12,弦AD平分∠BAC,则sin∠DAB=_____.
【答案】![]()
【解析】
作辅助线,构建直角△ACF,先求BC和CE的长,利用平行相似证明△ACF∽△DEF,可得CF的长,从而计算AF的长,根据三角函数定义可得结论.
解:连接BC、OD,BC与OD交于点E,BC与AD交于F,
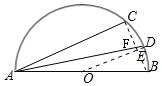
∵在半圆O中,AB是直径,
∴∠ACB=90°,∠CAB=2∠BAD,
∵AB=13,点C是半圆O上一点,AC=12,
∴BC=5,
∵弦AD平分∠BAC,
∴∠CAB=2∠BAD,
∵∠BOD=2∠BAD,
∴∠BAC=∠BOD,
∴AC∥OD,
∵AO=BO,
∴OE=![]() AC=6,
AC=6,
∴∠OEB=∠ACB,
∴∠OEB=90°,
∴BE=CE=![]() BC=
BC=![]() ,
,
∵DE∥AC,
∴△ACF∽△DEF,
∴![]() =
=![]() ,
,
∵OE=6,OD=![]() ,
,
∴DE=![]() ,
,
∴![]() =
=![]() =24,
=24,
∴CF=24EF,
∵CE=![]() ,
,
∴CF=![]() CE=
CE=![]() ×
×![]() =
=![]() ,
,
∴AF=![]() =
=![]() ,
,
∴sin∠DAF=sin∠CAF=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;
(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+(m﹣3)x﹣m+2的图象交x轴正半轴于点A,交x轴负半轴于点B,交y轴于点C.
(1)求m的取值范围;
(2)若△ABC恰为等腰三角形,求m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点E在线段AC上,连接BE,点D在直线BC上,且CE=CD,连接ED、AD,点F是BE的中点,连接FA、FD.
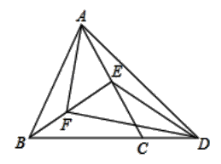
(1)若CD=6,BC=10,求△BEC的面积;
(2)当AE=CE时,求证:AD=2AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学有库存1800套旧桌凳,修理后捐助贫困山区学校.现有甲,乙两个木工组都想承揽这项业务.经协商后得知:甲木工组每天修理的桌凳套数是乙木工组每天修理桌凳套数的![]() ,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
(1)求甲,乙两木工组单独修理这批桌凳的天数;
(2)现有三种修理方案供选择:方案一,由甲木工组单独修理这批桌凳;方案二,由乙木工组单独修理这批桌凳;方案三,由甲,乙两个木工组共同合作修理这批桌凳.请计算说明哪种方案学校付的修理费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=()
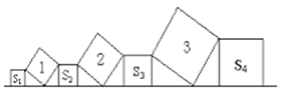
A. 5 B. 4 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
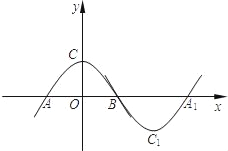
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com