
【题目】如图,E、F分别是正方形ABCD的边AD、CD上的点,且AE=DF,AF、BE相交于点P,设AB=![]() ,AE=
,AE=![]()
![]() ,则下列结论:①△ABE≌△DAF;②AF⊥BE;③
,则下列结论:①△ABE≌△DAF;②AF⊥BE;③![]() ;④若
;④若![]() ,连接BF,则tan∠EBF=
,连接BF,则tan∠EBF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
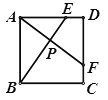
【答案】①②③④
【解析】分析:①根据正方形的性质得AB=AD=DC,∠BAD=∠D=90°,又EA=DF,根据“SAS”可判断△ABE≌△DAF,②利用∠FAD+∠FAB=90°得到∠ABE+∠FAB=90°,则AE⊥BF;③利用APE∽△ADF可得![]() ,故可求解;④分别求出BE、AP、BP、PE的长,即可求解.
,故可求解;④分别求出BE、AP、BP、PE的长,即可求解.
详解: ∵四边形ABCD为正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
在△ABE和△DAF中
 ,
,
∴△ABE≌△DAF,故①正确;
∴∠ABE=∠FAD,
而∠FAD+∠FAB=90°,
∴∠ABE+∠FAB=90°,
∴∠APB=90°,
∴AF⊥BE,所以②正确;
由①得∠AEB=∠DFA
∴APE∽△ADF
∴![]()
∴![]()
∴![]() ,故③正确;
,故③正确;
连接BF,如图:

∵![]()
∴在Rt△ABE中,BE=![]()
∴AP= ,
,![]()
∴FP=![]()
∴tan∠EBF=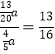 ,故④正确.
,故④正确.
故答案为:①②③④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2018个正方形的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是一条射线,
是一条射线,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线.
的平分线.
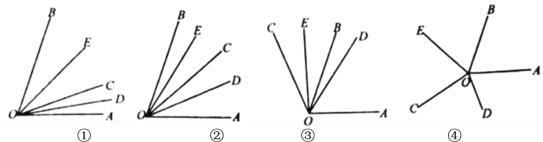
(1)如图①,当![]() 时,则
时,则![]() 的度数为________________;
的度数为________________;
(2)如图②,当射线![]() 在
在![]() 内绕
内绕![]() 点旋转时,
点旋转时,![]() 、
、![]() 、
、![]() 三角之间有怎样的数量关系?并说明理由;
三角之间有怎样的数量关系?并说明理由;
(3)当射线![]() 在
在![]() 外如图③所示位置时,(2)中三个角:
外如图③所示位置时,(2)中三个角:![]() 、
、![]() 、
、![]() 之间数量关系的结论是否还成立?给出结论并说明理由;
之间数量关系的结论是否还成立?给出结论并说明理由;
(4)当射线![]() 在
在![]() 外如图④所示位置时,
外如图④所示位置时,![]() 、
、![]() 、
、![]() 之间数量关系是____________.
之间数量关系是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:3x+5=x+2请按所给导语,填写完整.
解:移项,得3x____=2____,(依据:_____).
合并同类项,得______,
系数化为1,得_____,(依据:______).
(2)解方程:2(x+15)=18﹣3(x﹣9).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接浙江省中小学生健康体质测试,某学校开展“健康校园,阳光跳绳”活动,为此学校准备购置A,B,C三种跳绳.已知某厂家的跳绳的规格与价格如下表:
A绳子 | B绳子 | C绳子 | |
长度(米) | 8 | 6 | 4 |
单价(元/条) | 12 | 8 | 6 |
(1)已知购买A,B两种绳子共20条花了180元,问A,B两种绳子各购买了多少条?
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
(3)若该厂家有一根长200米的绳子,现将其裁成A,B,C三种绳子共40条(没有剩余)销售给学校,学校要求A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,请直接写出所有的裁剪方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面的5个时钟显示了同一时刻国外四个城市时间和北京时间,右图给出了国外四个城市与北京的时差,则下图中的时钟对应的城市依次是_____________________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则6小时可到达乙地.
(1)写出时间t(时)关于速度v(千米/时)的函数关系式,并画出函数图象.
(2)若这辆汽车需在5小时内从甲地到乙地,则此时汽车的平均速度至少应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售甲、乙两种运动鞋,2018年这两种鞋共卖出11000双。2019年甲种运动鞋卖出的数量比2018年增加6%,乙种运动鞋卖出的数量比2018年减少5%,且这两种鞋的总销量增加了2%.
(1)求2018年甲、乙两种运动鞋各卖了多少双?
(2)某制鞋厂组织工人生产甲、乙两种运动鞋。原计划安排 ![]() 的工人生产甲种运动鞋,现抽调其中的16人去生产乙种运动鞋,已知每位工人一天可生产甲种运动鞋6双或乙种运动鞋4双,若调配后制成的两种运动鞋数量相等,求该鞋厂工人的人数。
的工人生产甲种运动鞋,现抽调其中的16人去生产乙种运动鞋,已知每位工人一天可生产甲种运动鞋6双或乙种运动鞋4双,若调配后制成的两种运动鞋数量相等,求该鞋厂工人的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com