
【题目】为了迎接浙江省中小学生健康体质测试,某学校开展“健康校园,阳光跳绳”活动,为此学校准备购置A,B,C三种跳绳.已知某厂家的跳绳的规格与价格如下表:
A绳子 | B绳子 | C绳子 | |
长度(米) | 8 | 6 | 4 |
单价(元/条) | 12 | 8 | 6 |
(1)已知购买A,B两种绳子共20条花了180元,问A,B两种绳子各购买了多少条?
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
(3)若该厂家有一根长200米的绳子,现将其裁成A,B,C三种绳子共40条(没有剩余)销售给学校,学校要求A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,请直接写出所有的裁剪方案.
【答案】(1)A种绳子买了5条,B种绳子买了15条;(2)B种绳子最多可加工6条;(3)A、B、C三种绳子分别为5条、10条、25条或者6条、8条、26条.
【解析】
(1)设A种绳子买了x条,B种绳子买了y条,根据A,B两种绳子共20条;A,B两种绳子共花了180元列方程组求出x、y的值即可;
(2)设A种绳子裁了a条,C种绳子裁了c条.由裁成A,C两种绳子销售总价为240元得到:c=40﹣2a,然后求得B种绳子的总长度,进而可得答案.
(3)设A种绳子裁了m条,B种绳子裁了n条,C种绳子裁了t条.根据题意列方程组可得n=20﹣2m,根据A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,列不等式可求出m的取值范围,根据m为整数可得m的值,进而得答案.
(1)设A种绳子买了x条,B种绳子买了y条.
则![]() ,
,
解得![]() .
.
答:A种绳子买了5条,B种绳子买了15条;
(2)设A种绳子裁了a条,C种绳子裁了c条.
则12a+6c=240,化简得c=40﹣2a.
B种绳子的总长度为:200﹣8a﹣4c=200﹣8a﹣4(40﹣2a)=40(米)
∵B种绳子的长度为6米,
∴![]() =6…4,
=6…4,
∴B种绳子最多可加工6条.
(3)设A种绳子裁了m条,B种绳子裁了n条,C种绳子裁了t条.
∵一根长200米的绳子,现将其裁成A,B,C三种绳子共40条(没有剩余)
∴![]() ,
,
消去t得:2m+n=20,即n=20﹣2m,
∵A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,
∴![]() <m<n,
<m<n,
∴10﹣m≤m<20﹣2m,
解得:5≤m<![]() ,
,
∴m=5或6,
当m=5时,n=20﹣10=10,t=40﹣5﹣10=5;
当m=6时,n=20﹣12=8,t=40﹣6﹣8=26;
答:A、B、C三种绳子分别为5条、10条、25条或者6条、8条、26条.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,则下列结论中不正确的是( )
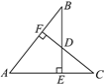
A. △ABE≌△ACF B. 点D在∠BAC的平分线上
C. △BDF≌△CDE D. D是BE的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:

(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
查看答案和解析>>
科目:初中数学 来源: 题型:
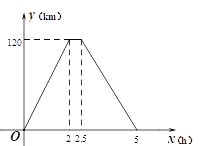
【题目】在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回甲地.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的关系如图所示.
根据图像回答下列问题:
(1)汽车在乙地卸货停留 (h);
(2)求汽车返回甲城时y与x的函数解析式,并写出定义域;
(3)求这辆汽车从甲地出发4 h时与甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.
(1)①若以B为原点.写出点A,D,C所对应的数,并计算p的值;
②若以D为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
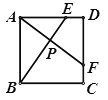
【题目】如图,E、F分别是正方形ABCD的边AD、CD上的点,且AE=DF,AF、BE相交于点P,设AB=![]() ,AE=
,AE=![]()
![]() ,则下列结论:①△ABE≌△DAF;②AF⊥BE;③
,则下列结论:①△ABE≌△DAF;②AF⊥BE;③![]() ;④若
;④若![]() ,连接BF,则tan∠EBF=
,连接BF,则tan∠EBF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的不完整统计表,根据表中信息,回答下列问题:
喜爱的电视节目类型 | 人数 | 频率 |
新闻 | 4 | 0.08 |
体育 | / | / |
动画 | 15 | / |
娱乐 | 18 | 0.36 |
戏曲 | / | 0.06 |
(1)本次共调查了_______名学生,若将各类电视节目喜爱的人数所占比例绘制成扇形统计图,则“喜爱动画”对应扇形的圆心角度数是_______;
(2)该校共有2000名学生,根据调查结果估计该校“喜爱体育”节目的学生人数;
(3)在此次问卷调查中,甲、乙两班分别有![]() 人喜爱新闻节目,若从这
人喜爱新闻节目,若从这![]() 人中随机抽取
人中随机抽取![]() 人去参加“新闻小记者”培训,求抽取的
人去参加“新闻小记者”培训,求抽取的![]() 人来自不同班级的概率.
人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,且
,且![]() 、
、![]() 、
、![]() 分别是点A. B. C在数轴上对应的数.
分别是点A. B. C在数轴上对应的数.

(1)写出![]() =___;
=___;![]() =___;
=___;![]() =___.
=___.
(2)若甲、乙、丙三个动点分别从A.B.C三点同时出发沿数轴负方向运动,它们的速度分别是1、2、4,(单位/秒),运行![]() 秒后,甲、乙、丙三个动点对应的位置分别为:
秒后,甲、乙、丙三个动点对应的位置分别为:![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求式子
时,求式子![]() 的值.
的值.
(3)若甲、乙、丙三个动点分别从A,B,C三点同时出发沿数轴正方向运动,它们的速度分别是1,2,4(单位/秒),运动多长时间后,乙与甲、丙等距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织360名师生外出活动,计划租用甲、乙两种型号的客车;经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)已知师生行李打包后共有164件,若租用10辆甲、乙两种型号的客车,请你帮助设计出该校所有可行的租车方案;
(2)若师生行李打包后共有m件,且170 < m ≤ 184,如果所租车辆刚好把所有师生和行李载走(每辆车均以最多承载量载满),求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com