
【题目】通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图(1)在△ABC中,AB=AC,底角B的邻对记作canB,这时canB=底边/腰=![]() ,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
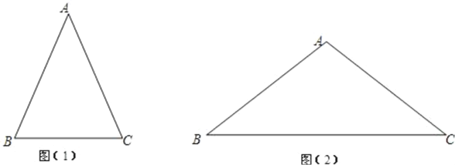
(1)can30°= ;
(2)如图(2),已知在△ABC中,AB=AC,canB=![]() ,S△ABC=24,求△ABC的周长.
,S△ABC=24,求△ABC的周长.
【答案】(1)![]() ;(2)18
;(2)18![]()
【解析】
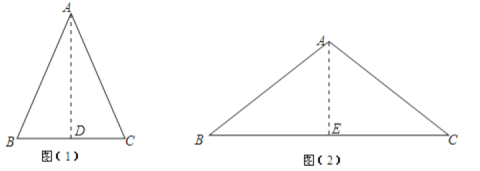
(1)过点A作AD⊥BC于点D,根据∠B=30°,可得出BD=![]() AB,结合等腰三角形的性质可得出BC=
AB,结合等腰三角形的性质可得出BC=![]() AB,继而得出canB;
AB,继而得出canB;
(2)过点A作AE⊥BC于点E,根据canB=![]() ,设BC=8x,AB=5x,再由S△ABC=24,可得出x的值,继而求出周长.
,设BC=8x,AB=5x,再由S△ABC=24,可得出x的值,继而求出周长.
解:(1)过点A作AD⊥BC于点D,
∵∠B=30°,
∴cos∠B=![]() =
=![]() ,
,
∴BD=![]() AB,
AB,
∵△ABC是等腰三角形,
∴BC=2BD=![]() AB,
AB,
∴can30°=![]() =
=![]() ;
;
故答案为:![]() ;
;
(2)过点A作AE⊥BC于点E,
∵canB=![]() ,则可设BC=8x,AB=5x,
,则可设BC=8x,AB=5x,
∴AE=![]() =3x,
=3x,
∵S△ABC=24,
∴![]() BC×AE=12x2=24,
BC×AE=12x2=24,
解得:x=![]() ,
,
∴AB=AC=5![]() ,BC=8
,BC=8![]() ,
,
∴可得△ABC的周长为18![]() .
.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
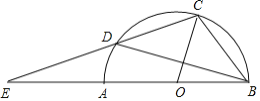
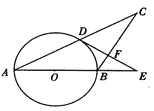
【题目】如图,半圆的半径OC=2,线段BC与CD是半圆的两条弦,BC=CD,延长CD交直径BA的延长线于点E,若AE=2,则弦BD的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)

查看答案和解析>>
科目:初中数学 来源: 题型:
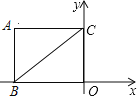
【题目】如图,平面直角坐标系中,矩形ABOC的边BO,CO分别在x轴,y轴上,A点的坐标为(﹣8,6),点P在矩形ABOC的内部,点E在BO边上,满足△PBE∽△CBO,当△APC是等腰三角形时,P点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 在
在![]() 上.以点
上.以点![]() 为圆心,
为圆心,![]() 为半径画弧,交
为半径画弧,交![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ;再以点
;再以点![]() 为圆心,
为圆心,![]() 为半径画弧,交
为半径画弧,交![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ;再以点
;再以点![]() 为圆心,
为圆心,![]() 为半径画弧,交
为半径画弧,交![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ;…按照这样的方法一直画下去,得到点
;…按照这样的方法一直画下去,得到点![]() ,若之后就不能再画出符合要求的点
,若之后就不能再画出符合要求的点![]() ,则
,则![]() 等于(
等于(

A.13B.12C.11D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
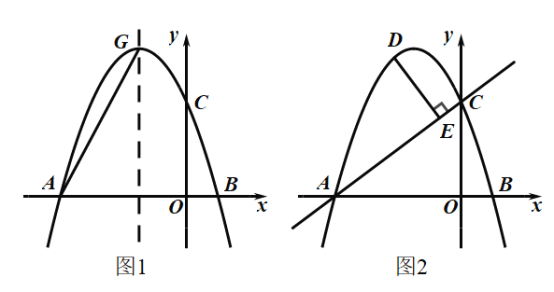
(1)求抛物线的解析式;
(2)如图1,抛物线的对称轴交抛物线于点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 坐标;若不存在,请说明理由;
坐标;若不存在,请说明理由;
(3)如图2,点![]() 为直线
为直线![]() 上方抛物线上的动点,
上方抛物线上的动点,![]() 于点
于点![]() ,求线段
,求线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC, 交AB的延长线于E,垂足为F.
(1)求证:直线DE是⊙O的切线;
(2)当AB=5,AC=8时,求cosE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com