
【题目】已知二次函数![]() 的图象如图所示,下列结论,正确的有( )个
的图象如图所示,下列结论,正确的有( )个
①![]() ②
②![]() ③
③![]() ④
④![]()
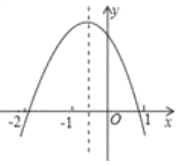
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
由抛物线开口方向得a<0,由抛物线的对称性得到-1<![]() <0,,则b<0,由抛物线与y轴交于正半轴得到c>0,所以abc>0,于是可对①进行判断;根据对称轴的位置得到-1<
<0,,则b<0,由抛物线与y轴交于正半轴得到c>0,所以abc>0,于是可对①进行判断;根据对称轴的位置得到-1<![]() <0,利用a<0变形得到b>2a,则可对②进行判断;根据图象即可得出x= -2时,y=4 a-2b+c<0,则可③进行判断;根据图象知道当x=1时,y=a+b+c<0,x=-1时,y=a-b+c>0,利用平方差公式可得(a+c)2-b2=(a+c+b)(a+c-b)<0,则可对④进行判断.
<0,利用a<0变形得到b>2a,则可对②进行判断;根据图象即可得出x= -2时,y=4 a-2b+c<0,则可③进行判断;根据图象知道当x=1时,y=a+b+c<0,x=-1时,y=a-b+c>0,利用平方差公式可得(a+c)2-b2=(a+c+b)(a+c-b)<0,则可对④进行判断.
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴与直线x=-1之间,即-1<![]() <0,
<0,
∴b<0,
∵抛物线与y轴交于正半轴,则c>0.
所以abc>0.
故①正确.
∵-1<![]() <0,a<0,
<0,a<0,
∴b>2a,即2a-b<0,所以②正确;
根据图象可得:x= -2时,y=4 a-2b+c<0,所以③正确;
根据图象知道当x=1时,y=a+b+c<0,
根据图象知道当x=-1时,y=a-b+c>0,
所以 (a+c)2-b2=(a+c+b)(a+c-b)<0.
所以 (a+c)2<b2.
故④错误.
故正确的有①②③.
故选:C.


科目:初中数学 来源: 题型:
【题目】通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图(1)在△ABC中,AB=AC,底角B的邻对记作canB,这时canB=底边/腰=![]() ,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
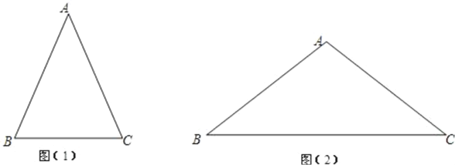
(1)can30°= ;
(2)如图(2),已知在△ABC中,AB=AC,canB=![]() ,S△ABC=24,求△ABC的周长.
,S△ABC=24,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,反比例函数
,反比例函数![]() (a,b,k是常数,且
(a,b,k是常数,且![]() ),若其中一部分x,y的对应值如表:则不等式
),若其中一部分x,y的对应值如表:则不等式![]() 的解集是_________.
的解集是_________.
x |
|
|
|
| 1 | 2 | 3 | 4 |
| 3 | 2 | 1 | 0 |
|
|
|
|
|
| 2 | 3 | 6 |
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了深入学习社会主义核心价值观,对本校学生进行了一次相关知识的测试,随机抽取了部分学生的测试成绩进行统计(根据成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个组,
五个组,![]() 表示测试成绩,
表示测试成绩,![]() 组:
组:![]() ;
;![]() 组:
组:![]() ;
;![]() 组:
组:![]() ;
;![]() 组:
组:![]() ;
;![]() 组:
组:![]() ),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
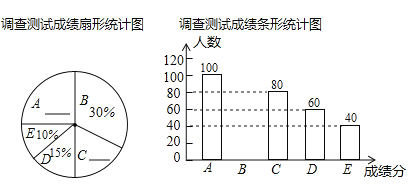
(1)抽取的学生共有______人,请将两幅统计图补充完整;
(2)抽取的测试成绩的中位数落在______组内;
(3)本次测试成绩在80分以上(含80分)为优秀,若该校初三学生共有1200人,请估计该校初三测试成绩为优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x2<1,有下列结论:①b2﹣4ac>0;②4a﹣2b+c>﹣1;③﹣3<x1<﹣2;④当m为任意实数时,a﹣b≤am2+bm;⑤3a+c=0.其中,正确的结论有( )
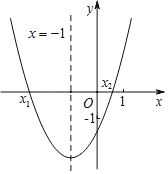
A.②③④B.①③⑤C.②④⑤D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点E是AD的中点,连接CE,并延长CE与BA的延长线交于点F, 若∠BCF=90°,则∠D的度数为( )
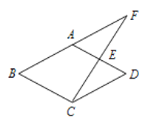
A.60°B.55°C.45°D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
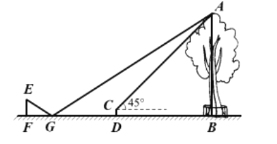
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.

(1)判断AF和⊙O的位置关系并说明理由.
(2)若∠ABC=60°,BC=1cm,求阴影部分的面积.(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com