
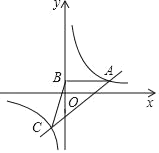
【题目】经过点A(4,1)的直线与反比例函数y=![]() 的图象交于点A、C,AB⊥y轴,垂足为B,连接BC.
的图象交于点A、C,AB⊥y轴,垂足为B,连接BC.
(1)求反比例函数的表达式;
(2)若△ABC的面积为6,求直线AC的函数表达式;
(3)在(2)的条件下,点P在双曲线位于第一象限的图象上,若∠PAC=90°,则点P的坐标是 .
【答案】(1)反比例函数的表达式为y=![]() (2)直线AC的函数表达式为y=
(2)直线AC的函数表达式为y=![]() x﹣1;(3)(
x﹣1;(3)(![]() ,8).
,8).
【解析】
(1)将点A坐标代入反比例函数表达式中,即可得出结论;
(2)先求出AB,设出点C的纵坐标,利用△ABC的面积为6,求出点C纵坐标,再代入反比例函数表达式中,求出点C坐标,最后用待定系数法求出直线AC的解析式;
(3)先求出直线AP的解析式,再和反比例函数解析式联立求解即可得出结论.
解:(1)∵点A(4,1)在反比例函数y=![]() 的图象上,
的图象上,
∴k=4×1=4,
∴反比例函数的表达式为y=![]() ;
;
(2)设点C的纵坐标为m,
∵AB⊥y轴,A(4,1),
∴AB=4,
∵△ABC的面积为6,
∴![]() AB×(1﹣m)=6,
AB×(1﹣m)=6,
∴m=﹣2,
由(1)知,反比例函数的表达式为y=![]() ,
,
∴点C的纵坐标为:﹣2,
∴点C(﹣2,﹣2),
设直线AC的解析式为y=k'x+b,
将点A(4,1),C(﹣2,﹣2)代入y=k'x+b中,![]() ,
,
∴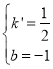 ,
,
∴直线AC的函数表达式为y=![]() x﹣1;
x﹣1;
(3)由(2)知直线AC的函数表达式为y=![]() x﹣1,
x﹣1,
∵∠PAC=90°,
∴AC⊥AP,
∴设直线AP的解析式为y=﹣2x+b',
将A(4,1)代入y=﹣2x+b'中,﹣8+b'=1,
∴b'=9,
∴直线AP的解析式为y=﹣2x+9①,
由(1)知,反比例函数的表达式为y=![]() ②,
②,
联立①②解得,![]() (舍)或
(舍)或![]() ,
,
∴点P的坐标为(![]() ,8),
,8),
故答案为:(![]() ,8).
,8).


科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,对于以下说法:①b2﹣4ac>0②x=x0是方程ax2+bx+c=y0的解③x1<x0<x2④a(x0﹣x1)(x0﹣x2)<0其中正确的是( )
A.①③④B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店A类笔的标价是B类笔标价的1.2倍,某顾客用240元买笔,能单独购买A笔的数量恰好比单独购买B类笔的数量少4支.
(1)求A,B两类笔的标价;
(2)若A类笔的进价为8元/支,B类笔的进价为7元/支.文具店老板准备用不超过760元购进两类笔共100支,应如何进货才能获得最大利润?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2011年高中招生考试,某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行,绘制成了如下两幅不完整的统计图,请根据图中所给信息,下列问题:
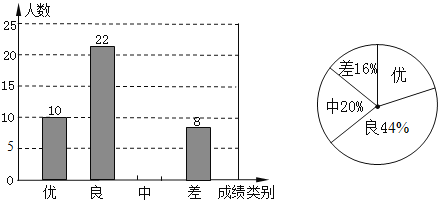
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是 72 度;
(3)学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市九年级学生升学考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(![]() :40分;
:40分;![]() :39-35分;
:39-35分;![]() :34-30分;
:34-30分;![]() :29-20分;
:29-20分;![]() :19-0分) 统计如右表。根据上面提供的信息,回答下列问题:
:19-0分) 统计如右表。根据上面提供的信息,回答下列问题:
(1)在统计表中,![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问:甲同学的体育成绩应在 分数段内(填相应分数段的字母).
(3)若把成绩在![]() 分以上(含
分以上(含![]() 分)定为优秀,则我市今年8000名九年级学生中体育成绩为优秀的学生人数约有 .名.
分)定为优秀,则我市今年8000名九年级学生中体育成绩为优秀的学生人数约有 .名.
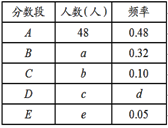
查看答案和解析>>
科目:初中数学 来源: 题型:
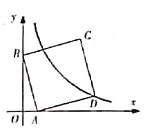
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,以
两点,以![]() 为边在第一象限作正方形
为边在第一象限作正方形![]() 沿
沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度后,点
个单位长度后,点![]() 恰好落在双曲线上,则
恰好落在双曲线上,则![]() 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是□ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E、连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )个.
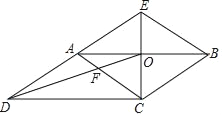
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=![]() (x>0)的图象经过A,B两点.若点A的坐标为(n,1),则 k的值为______.
(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则 k的值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com