
����Ŀ����ͼ��������4��4���߳�Ϊ1���������У���֪��ABC����������A��B��C�ڸ���ϣ���ֱ𰴲�ͬҪ�������������һ�����D����д����D�����꣮
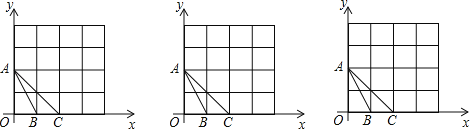
��1������ABC�Ƶ�C˳ʱ����ת90����������ת�����õ������Σ���A��ת�����ΪD��
��2������A��B��C������һ�������ߣ����ҵ���D��ʹ��DҲ���������������ϣ�
��3������A��B��C������һ��Բ�����ҵ�һ��������Ϊ2�ĵ�D��ʹ��DҲ�������Բ�ϣ�
�ٵ�D������Ϊ�� ����
�ڵ�D������Ϊ�� ����
�۵�D������Ϊ�� ����
���𰸡���1����ͼ���������� ��2����D��3��2������3���٣�4��2�����ڣ�3��2�����ۣ�2��3����
��������
��1����ͼ����B�Ķ�Ӧ��ΪB������A�Ķ�Ӧ��Ϊ��D��4��2����
��2�������ߵĶԳ�����BC���д����ϣ����D��A���ں����Գ���Գƣ�������⣻
��3��AC�д��ߵı���ʽΪ��y=x��BC���д���Ϊ��x=![]() ����Բ��OΪ����
����Բ��OΪ����![]() ��
��![]() �������D��2��m������OD=OB��������⣮
�������D��2��m������OD=OB��������⣮
��1����ͼ����B�Ķ�Ӧ��ΪB�䣬��A�Ķ�Ӧ��Ϊ��D��4��2����
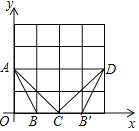
�ʢٴ�Ϊ����4��2����
��2�������ߵĶԳ�����BC���д����ϣ����D��A���ں����Գ���Գƣ�
�ʵ�D��3��2����
�ʢڵĴ�Ϊ����3��2����
��3��AC�д��ߵı���ʽΪ��y��x��BC���д���Ϊ��x��![]() ��
��
��Բ��OΪ����![]() ��
��![]() �������D��2��m����
�������D��2��m����
��OD��OB����![]() ��2+��
��2+��![]() ��2����2��
��2����2��![]() ��2+��m��
��2+��m��![]() ��2��
��2��
��ã�m��0��3����ȥ0����
�ʵ�D��2��3����
�ʢ۵Ĵ�Ϊ��2��3����


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ����װ�������ֱ�д������6��-2��7��С�����ǵ���״����С���ʵص���ȫ��ͬ���ȴӺ��������ȡ��һ��С�������ֺ�Żغ��ӣ�ҡ�Ⱥ������ȡ��һ��С�������֣������û���״ͼ�ķ������������¼��ĸ��ʣ�
(1)����ȡ��С���ϵ�������ͬ��
(2)����ȡ��С���ϵ�����֮�ʹ���10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+3��a��0����x�ᣬy��ֱ��ڵ�A����1��0����B��3��0������C���㣮
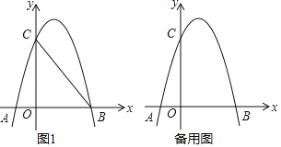
��1�����������ߵĽ���ʽ��
��2����D��2��m���ڵ�һ�����������ϣ�����BC��BD�����ʣ��ڶԳ����������������Ƿ����һ��P�������PBC����DBC��������ڣ��������P������ꣻ��������ڣ���˵�����ɣ�
��3����N�������ߵĶԳ����ϣ���M���������ϣ�����M��N��B��CΪ������ı�����ƽ���ı���ʱ����ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
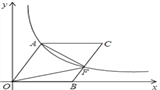
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬B��x���ϣ��ı���OACBΪƽ���ı��Σ���
��AOB=60�㣬����������![]() ��k��0���ڵ�һ�����ڹ���A������BC���ڵ�F����FΪBC���е㣬��S��AOF��12
��k��0���ڵ�һ�����ڹ���A������BC���ڵ�F����FΪBC���е㣬��S��AOF��12![]() ʱ��OA�ij�Ϊ____.
ʱ��OA�ij�Ϊ____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
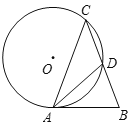
����Ŀ����ͼ���ڡ�ABC�У�AC=BC=2��D��BC���е㣬��A��C��D����ġ�O��AB�������ڵ�A�����O�İ뾶Ϊ( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ո���������ѧϰ���飬��ͨ���������һ�����ķ���̽��������θ�ʽ���������.
������С�յ�̽�����̣��벹������.
��1���������㣬���ֹ��ɣ�
����1��![]() ������2��
������2��![]() ������3��
������3��![]() ��
��
����4��______����һ�����������������������ӣ���
��2���۲졢���ɣ��ó����룺
���![]() Ϊ���������ú�
Ϊ���������ú�![]() ��ʽ�ӱ�ʾ���������ɣ�______��
��ʽ�ӱ�ʾ���������ɣ�______��
��3������֤���������ȷ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ո���������ѧϰ���飬��ͨ���������һ�����ķ���̽��������θ�ʽ���������.
������С�յ�̽�����̣��벹������.
��1���������㣬���ֹ��ɣ�
����1��![]() ������2��
������2��![]() ������3��
������3��![]() ��
��
����4��______����һ�����������������������ӣ���
��2���۲졢���ɣ��ó����룺
���![]() Ϊ���������ú�
Ϊ���������ú�![]() ��ʽ�ӱ�ʾ���������ɣ�______��
��ʽ�ӱ�ʾ���������ɣ�______��
��3������֤���������ȷ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
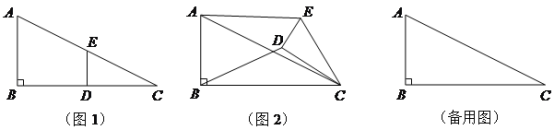
����Ŀ����10�֣���ͼ1����Rt��ABC�У���B=90����BC=2AB=8����D��E�ֱ��DZ�BC��AC���е㣬����DE. ����EDC�Ƶ�C��˳ʱ�뷽����ת������ת��Ϊ��.
��1�����ⷢ��
�� ��![]() ʱ��
ʱ��![]() ���� ��
���� ��![]() ʱ��
ʱ��![]()
��2����չ̽��
���жϣ���0��ܦ���360��ʱ��![]() �Ĵ�С���ޱ仯�������ͼ2���������֤��.
�Ĵ�С���ޱ仯�������ͼ2���������֤��.
��3��������
����EDC��ת��A��D��E���㹲��ʱ��ֱ��д���߶�BD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У���
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��![]() ����
����![]() ������
������![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() .
.
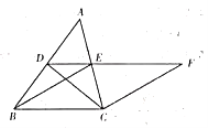
��1����֤���ı���![]() �����Σ�
������
��2���ڲ������κθ����ߺ���ĸ������£���ֱ��д��ͼ����![]() �����ȵ����������Σ�������
�����ȵ����������Σ�������![]() ��.
��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com