
【题目】小刚根据以往的学习经验,想通过由“特殊到一般”的方法探究下面二次根式的运算规律.
以下是小刚的探究过程,请补充完整.
(1)具体运算,发现规律:
特例1:![]() ;特例2:
;特例2:![]() ;特例3:
;特例3:![]() ;
;
特例4:______(举一个符合上述运算特征的例子);
(2)观察、归纳,得出猜想:
如果![]() 为正整数,用含
为正整数,用含![]() 的式子表示这个运算规律:______;
的式子表示这个运算规律:______;
(3)请你证明猜想的正确性.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
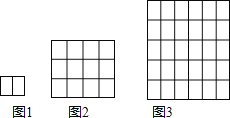
【题目】这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用_____木块才能把第四次所铺的完全围起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国内汽车市场中,国产 SUV 出现了持续不退的销售热潮 ,2019 年国产 SUV 销量排行榜完整版已经出炉,某品牌车型以惊人的销量成绩击退了所有虎视眈眈的对手,再次霸气登顶,下面是该品牌国产SUV分别在2018年与2019年7-11月的销售量对比表:
时间 | 7 月 | 8 月 | 9 月 | 10 月 | 11 月 |
2018 年(单位:万辆) | 2.8 | 3.9 | 3.5 | 4.4 | 5.4 |
2019 年(单位:万辆) | 3.8 | 3.9 | 4.5 | 4.9 | 5.4 |
(1)若从7月至11月中任选两个月,求其中至少有一个月这两年该国产品牌 SUV 销量相同的概率;
(2)若从2018年售出的每辆车获利3万元,2019年售出的每辆车获利2.5万元,试比较这两年7月至11月的月平均获利哪年高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列4×4(边长为1)的网格中,已知△ABC的三个顶点A,B,C在格点上,请分别按不同要求在网格中描出一个格点D,并写出点D的坐标.
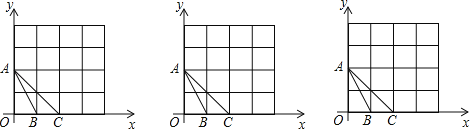
(1)将△ABC绕点C顺时针旋转90°,画出旋转后所得的三角形,点A旋转后落点为D;
(2)经过A,B,C三点有一条抛物线,请找到点D,使点D也落在这条抛物线上;
(3)经过A,B,C三点有一个圆,请找到一个横坐标为2的点D,使点D也落在这个圆上,
①点D的坐标为 ;
②点D的坐标为 ;
③点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:活动课上,某数学兴趣小组在操场看到马路上行驶的汽车,突发奇想:“想测量汽车的速度”.他们想到的方法是:如图,一人站在![]() 长且平行于公路(
长且平行于公路(![]() )的巨型广告牌(
)的巨型广告牌(![]() )前的点
)前的点![]() 处.广告牌恰好挡住了此人的视线,将看不到的那段公路记为
处.广告牌恰好挡住了此人的视线,将看不到的那段公路记为![]() .已知此人到广告牌和广告牌到公路的距离分别是
.已知此人到广告牌和广告牌到公路的距离分别是![]() 和
和![]() ,一辆匀速行驶的汽车经过公路
,一辆匀速行驶的汽车经过公路![]() 段的时间是
段的时间是![]() (不计汽车长度),请作答:
(不计汽车长度),请作答:
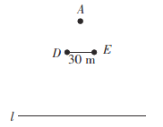
(1)请在图上画出线段![]() ;
;
(2)求该汽车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
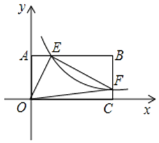
【题目】如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点![]() 不与点A、B重合
不与点A、B重合![]() ,过点E的反比例函数
,过点E的反比例函数![]() 的图象与边BC交于点F
的图象与边BC交于点F
![]() 若
若![]() 的面积为
的面积为![]() ,且
,且![]() ,求k的值;
,求k的值;
![]() 若
若![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象与边AB、边BC交于点E和F,当
的图象与边AB、边BC交于点E和F,当![]() 沿EF折叠,点B恰好落在OC上,求k的值.
沿EF折叠,点B恰好落在OC上,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里有若干个小球,它们除了颜色外,其它都相同,甲同学从袋子里随机摸出一个球,记下颜色后放回袋子里,摇匀后再次随机摸出一个球,记下颜色,…,甲同学反复大量实验后,根据白球出现的频率绘制了如图所示的统计图,则下列说法正确的是( )
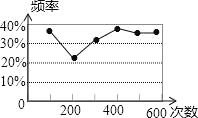
A. 袋子一定有三个白球
B. 袋子中白球占小球总数的十分之三
C. 再摸三次球,一定有一次是白球
D. 再摸1000次,摸出白球的次数会接近330次
查看答案和解析>>
科目:初中数学 来源: 题型:
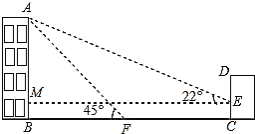
【题目】如图,某办公楼AB的右边有一建筑物CD,在建设物CD离地面2米高的点E处观测办公楼顶A点,测得的仰角![]() =
=![]() ,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角
,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角![]() =
=![]() (B,F,C在一条直线上).
(B,F,C在一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB>AD,∠A=60°,
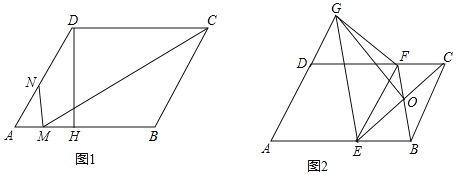
(1)如图1,过点D作DH⊥AB于点H,MC平分∠DCB交AB边于点M,过M作MN⊥AB交AD边于点N,AN:ND=2:3,平行四边形ABCD的面积为60![]() ,求MN的长度.
,求MN的长度.
(2)如图2,E、F分别为边AB、CD上一点,且AE=AD=DF,连接BF、EC交于点O,G为AD延长线上一点,连接GE、GF和GO,若∠GFD=∠EFB,求证:GO⊥EC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com