
【题目】如图,在平行四边形ABCD中,AB>AD,∠A=60°,
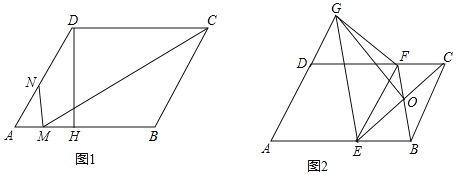
(1)如图1,过点D作DH⊥AB于点H,MC平分∠DCB交AB边于点M,过M作MN⊥AB交AD边于点N,AN:ND=2:3,平行四边形ABCD的面积为60![]() ,求MN的长度.
,求MN的长度.
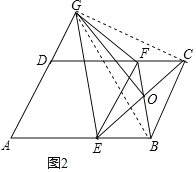
(2)如图2,E、F分别为边AB、CD上一点,且AE=AD=DF,连接BF、EC交于点O,G为AD延长线上一点,连接GE、GF和GO,若∠GFD=∠EFB,求证:GO⊥EC.
【答案】(1)2![]() ;(2)见解析
;(2)见解析
【解析】
(1)设AN=2x,DN=3x,得到AD=5x,解直角三角形得到AM=x,MN![]() x,根据平行四边形的性质得到BC=AD,CD∥AB根据等腰三角形的性质得到BM=BC=AD=5x,根据平行四边形的面积列方程即可得到结论;
x,根据平行四边形的性质得到BC=AD,CD∥AB根据等腰三角形的性质得到BM=BC=AD=5x,根据平行四边形的面积列方程即可得到结论;
(2)连接CG,BG,根据平行四边形的性质得到AB=CD,AB∥CD,推出四边形AEFD是菱形,根据全等三角形的性质得到DG=BE,得到△ABG是等边三角形,求得BG=AB=CD,∠ABG=60°,推出四边形EBCF是平行四边形,根据等腰三角形的性质即可得到结论.
(1)∵AN:ND=2:3,
∴设AN=2x,则DN=3x,
∴AD=5x.
∵MN⊥AB,
∴∠AMN=90°.
∵∠A=60°,
∴AM=x,MN![]() x.
x.
∵DH⊥AB,
∴DH![]() AD
AD![]() x.
x.
∵四边形ABCD是平行四边形,
∴BC=AD,CD∥AB,
∴∠DCM=∠BMC.
∵MC平分∠DCB,
∴∠DCM=∠BCM,
∴∠CMB=∠BCM,
∴BM=BC=AD=5x,
∴AB=6x.
∵平行四边形ABCD的面积为60![]() ,
,
∴ABDH=6x![]() x=60
x=60![]() ,
,
∴x=2(负值舍去),
∴MN的长度为2![]() ;
;
(2)连接CG,BG.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∵AE=AD=DF,
∴四边形AEFD是菱形,
∴AD=EF=DF,AD∥EF,
∴∠BEF=∠A=∠CDG=60°.
在△FDG与△FEB中,
∵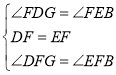 ,
,
∴△FDG≌△FEB(ASA),
∴DG=BE,
∴AG=AB,
∴△ABG是等边三角形,
∴BG=AB=CD,∠ABG=60°.
在△BGE与△CDG中,
∵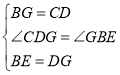 ,
,
∴△BGE≌△CDG,
∴GE=GC.
∵AD∥EF∥BC,AD=EF=BC,
∴四边形EBCF是平行四边形,
∴CO=OE,
∴GO⊥EC.


科目:初中数学 来源: 题型:
【题目】小刚根据以往的学习经验,想通过由“特殊到一般”的方法探究下面二次根式的运算规律.
以下是小刚的探究过程,请补充完整.
(1)具体运算,发现规律:
特例1:![]() ;特例2:
;特例2:![]() ;特例3:
;特例3:![]() ;
;
特例4:______(举一个符合上述运算特征的例子);
(2)观察、归纳,得出猜想:
如果![]() 为正整数,用含
为正整数,用含![]() 的式子表示这个运算规律:______;
的式子表示这个运算规律:______;
(3)请你证明猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 是中线,
是中线,![]() 于点G,交
于点G,交![]() 于点F,交
于点F,交![]() 于点M,
于点M,![]() 的延长线交
的延长线交![]() 于点H.
于点H.
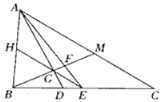
(1)图中与线段![]() 相等的线段是________;
相等的线段是________;
(2)求证:点H为线段![]() 的中点;
的中点;
(3)若![]() ,探究线段
,探究线段![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
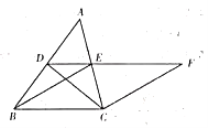
(1)求证:四边形![]() 是菱形;
是菱形;
(2)在不添加任何辅助线和字母的情况下,请直接写出图中与![]() 面积相等的所有三角形(不包括
面积相等的所有三角形(不包括![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我校举行的小科技创新发明比赛中,共有60人获奖,组委会原计划按照一等奖5人,二等奖15人,三等奖40人进行奖励.后来经学校研究决定,在该项奖励总奖金不变的情况下,各等级获奖人数实际调整为:一等奖10人,二等奖20人,三等奖30人,调整后一等奖每人奖金降低80元,二等奖每人奖金降低50元,三等奖每人奖金降低30元,调整前二等奖每人奖金比三等奖每人奖金多70元,则调整后一等奖每人奖金比二等奖每人奖金多____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:在数学课上,老师提出如下问题:
尺规作图,过圆外一点作圆的切线.
已知:⊙O和点P
求过点P的⊙O的切线
小涵的主要作法如下:
如图,(1)连结OP,作线段OP的中点A;
(2)以A为圆心,OA长为半径作圆,交⊙O于点B,C;
(3)作直线PB和PC.
所以PB和PC就是所求的切线.
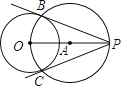
老师说:“小涵的做法正确的.”
请回答:小涵的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
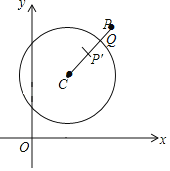
【题目】如图,在平面直角坐标系xOy 中,点P是⊙C外一点,连接CP交⊙C于点Q,点P关于点Q的对称点为P′,当点P′在线段CQ上时,称点P为⊙C“友好点”.已知A(1,0),B(0,2),C(3,3)
(1)当⊙O的半径为1时,
①点A,B,C中是⊙O“友好点”的是 ;
②已知点M在直线y=﹣![]() x+2 上,且点M是⊙O“友好点”,求点M的横坐标m的取值范围;
x+2 上,且点M是⊙O“友好点”,求点M的横坐标m的取值范围;
(2)已知点D![]() ,连接BC,BD,CD,⊙T的圆心为T(t,﹣1),半径为1,若在△BCD上存在一点N,使点N是⊙T“友好点”,求圆心T的横坐标t的取值范围.
,连接BC,BD,CD,⊙T的圆心为T(t,﹣1),半径为1,若在△BCD上存在一点N,使点N是⊙T“友好点”,求圆心T的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=-1,点B的坐标为(1,0),则下列结论:①AB=4;②b2-4ac>0;③ab<0;④a2-ab+ac<0,其中正确的结论有( )个.
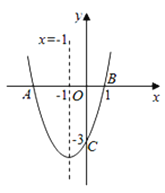
A. 3B. 4C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
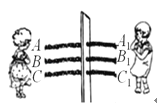
【题目】如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.
(1)问:“姐妹两人同时选中同一根绳子”这一事件是 事件,概率是 ;
(2)在互相看不见的条件下,姐姐先将左侧A、C两个绳端打成一个连结,则妹妹从右侧A1、B1、C1三个绳端中随机选两个打一个结(打结后仍能自由地通过木孔);请求出“姐姐抽动绳端B,能抽出由三根绳子连结成一根长绳”的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com