
【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)试验.
(1)她们在一次试验中共掷骰子60次,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
①填空:此次试验中“5点朝上”的频率为____;
②小红说:“根据试验,出现5点的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在试验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表法或画树状图的方法加以说明,并求出其最大概率
【答案】(1)①![]() ;②见详解;(2)
;②见详解;(2)![]() .
.
【解析】
试题(1)①让5出现的次数除以总次数即为所求的频率;②根据概率的意义,需要大量实验才行;
(2)列举出所有情况,比较两枚骰子朝上的点数之和的情况数,进而让最多的情况数除以所有情况数的即可.
试题解析:(1) ①![]()
②小红的说法不正确.理由:∵利用频率估计概率的试验次数必须比较多,重复试验,频率才慢慢接近概率,而她们的试验次数太少,没有代表性,∴小红的说法不正确.
(2)列表:
(1,6) | (2,6) | (3,6) | (4,6) | (5,6) | (6,6) |
(1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) |
(1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
(1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) |
(1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
(1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
共有36种等可能的结果,其中点数之和为7的结果数最多,有6种,
∴两枚骰子朝上的点数之和为7时,概率最大,最大概率为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,顶点为(![]() ,-
,-![]() )的抛物线y=ax2+bx+c过点M(2,0).
)的抛物线y=ax2+bx+c过点M(2,0).
(1)求抛线的表达式;
(2)点A是抛物线与x轴的交点(不与点M重合),点B是抛物线与y轴的交点,点C是直线y=x+1上一点(处于x轴下方),点D是反比例函数y=![]() (k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.
(k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解决后面的问题:
材料:因为二次三项式:
x2+(a+b)x+ab=(x+a)(x+b),
所以方程x2+(a+b)x+ab=0可以这样解:
(x+a)(x+b)=0,x+a=0或x+b=0,
∴x1=-a,x2=-b.
问题:
(1)(铁岭中考)如果三角形的两边长分别是方程x2-8x+15=0的两个根,那么连接这个三角形三边的中点,得到的三角形的周长可能是( )
A.5.5 B.5 C.4.5 D.4
(2)(广安中考)方程x2-3x+2=0的根是_____;
(3)(临沂中考)对于实数a,b,定义运算“﹡”:a﹡b=![]() ,例如4﹡2,因为4>2,所以4﹡2=42-4×2=8.若x1,x2是一元二次方程x2-5x+6=0的两个根,则x1﹡x2=_____;
,例如4﹡2,因为4>2,所以4﹡2=42-4×2=8.若x1,x2是一元二次方程x2-5x+6=0的两个根,则x1﹡x2=_____;
(4)用因式分解法解方程x2-kx-16=0时,得到的两根均为整数,则k的值可以为_____;
(5)已知实数x满足(x2-x)2-4(x2-x)-12=0,则代数式x2-x+1的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A.一个游戏中奖的概率是![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了了解全国中学生的心理健康状况,应采用普查的方式
C.一组数据0,1,2,1,1的众数和中位数都是1
D.若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
(1)求弦AC的长;
(2)求证:BC∥PA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.
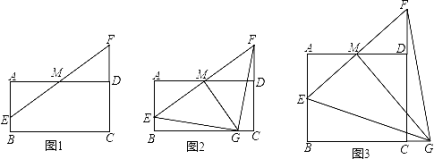
(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作 MG⊥EF交线段BC于点G,求证:△GEF是等腰直角三角形
(3)如图3,若AB=![]() ,过点M作 MG⊥EF交线段BC的延长线于点G.
,过点M作 MG⊥EF交线段BC的延长线于点G.
①直接写出线段AE长度的取值范围;
②判断△GEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com