
【题目】先阅读下列材料,然后解决后面的问题:
材料:因为二次三项式:
x2+(a+b)x+ab=(x+a)(x+b),
所以方程x2+(a+b)x+ab=0可以这样解:
(x+a)(x+b)=0,x+a=0或x+b=0,
∴x1=-a,x2=-b.
问题:
(1)(铁岭中考)如果三角形的两边长分别是方程x2-8x+15=0的两个根,那么连接这个三角形三边的中点,得到的三角形的周长可能是( )
A.5.5 B.5 C.4.5 D.4
(2)(广安中考)方程x2-3x+2=0的根是_____;
(3)(临沂中考)对于实数a,b,定义运算“﹡”:a﹡b=![]() ,例如4﹡2,因为4>2,所以4﹡2=42-4×2=8.若x1,x2是一元二次方程x2-5x+6=0的两个根,则x1﹡x2=_____;
,例如4﹡2,因为4>2,所以4﹡2=42-4×2=8.若x1,x2是一元二次方程x2-5x+6=0的两个根,则x1﹡x2=_____;
(4)用因式分解法解方程x2-kx-16=0时,得到的两根均为整数,则k的值可以为_____;
(5)已知实数x满足(x2-x)2-4(x2-x)-12=0,则代数式x2-x+1的值为_____.
【答案】(1)A;(2)1或2; (3)3或-3; (4)-15,-6,0,6,15; (5)7.
【解析】
试题![]() 首先解方程求得三角形的两边长,则第三边的范围可以求得,进而得到三角形的周长
首先解方程求得三角形的两边长,则第三边的范围可以求得,进而得到三角形的周长![]() 的范围,而连接这个三角形三边的中点,得到的三角形的周长一定是
的范围,而连接这个三角形三边的中点,得到的三角形的周长一定是![]() 的一半,从而求得中点三角形的周长的范围,从而确定.
的一半,从而求得中点三角形的周长的范围,从而确定.
![]() 由题已知的方程进行因式分解,将原式化为两式相乘的形式,再根据两式相乘值为0,这两式中至少有一式值为0,求出方程的解.
由题已知的方程进行因式分解,将原式化为两式相乘的形式,再根据两式相乘值为0,这两式中至少有一式值为0,求出方程的解.
![]() 解出方程
解出方程![]() 的两个根,再分类讨论即可.
的两个根,再分类讨论即可.
![]() 对式子进行因式分解,即可求出
对式子进行因式分解,即可求出![]() 的值.
的值.
![]() 由整体思想,用因式分解法解方程求出
由整体思想,用因式分解法解方程求出![]() 的值,就可以得出结论.
的值,就可以得出结论.
试题解析:![]() 解方程
解方程![]() 得:
得:![]()
则第三边c的范围是:2<c<8.
则三角形的周长l的范围是:10<l<16,
∴连接这个三角形三边的中点,得到的三角形的周长m的范围是:5<m<8.
故满足条件的只有A.
故选A.
![]() 因式分解得,(x1)(x2)=0,
因式分解得,(x1)(x2)=0,
解得![]()
故答案为:![]()
![]()
![]() 是一元二次方程
是一元二次方程![]() 的两个根,
的两个根,
∴(x3)(x2)=0,
解得:x=3或2,
①当![]() 时,x1﹡x2=323×2=3;
时,x1﹡x2=323×2=3;
②当![]() 时,x1﹡x2=3×232=3.
时,x1﹡x2=3×232=3.
故答案为:3或3.
![]()
![]()
![]()
![]() 或
或![]() 或
或![]()
故答案为:![]() 或
或![]() 或
或![]()
![]()
![]()
![]() 或
或![]()
![]() 或
或![]()
当![]() 时,
时,
![]() ,
,
![]() ∴此方程无实数解.
∴此方程无实数解.
当![]() 时,
时,
![]()
故答案为:![]()


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】设二次函数y=(x-x1)(x-x2) (x1,x2 为实数)
(1)甲求得当x=0时,y=0;当x=1时,y=0;乙求得当x=![]() 时,y=-
时,y=-![]() ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由。
,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由。
(2)写出二次函数图象的对称轴,并求出该函数的最小值(用含x1,x2的代数式表示)
(3)已知二次函数的图象经过(0,m),和(1,n)两点(m,n是实数),0<x1<x2<1时,求证:0<mn<![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c–3b<0;⑤a+b>n(an+b)(n≠1),其中正确的结论有( )
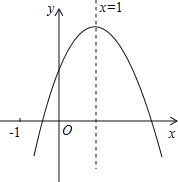
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
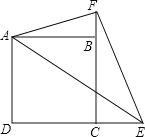
【题目】正方形ABCD中,点E在DC延长线上,点F在CB延长线上,∠EAF=45°,∠BAF=15°
(1)求证:DE﹣EF=BF;
(2)若AD=![]() ,求△AEF的面积.
,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A. S3>S4>S6 B. S6>S4>S3 C. S6>S3>S4 D. S4>S6>S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有9个红球和若干个白球,在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的个数:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色…,小明重复上述过程共摸了100次,其中40次摸到白球,请回答:
(1)口袋中的白球约有多少个?
(2)有一个游乐场,要按照上述红球、白球的比例配置彩球池,若彩球池里共有1200个球,则需准备多少个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)试验.
(1)她们在一次试验中共掷骰子60次,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
①填空:此次试验中“5点朝上”的频率为____;
②小红说:“根据试验,出现5点的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在试验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表法或画树状图的方法加以说明,并求出其最大概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )
A. (﹣4,3) B. (﹣3,4)
C. (3,﹣4) D. (4,﹣3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com