
【题目】正方形ABCD中,点E在DC延长线上,点F在CB延长线上,∠EAF=45°,∠BAF=15°
(1)求证:DE﹣EF=BF;
(2)若AD=![]() ,求△AEF的面积.
,求△AEF的面积.
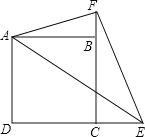
【答案】(1)证明见解析;(2)3![]() ﹣3.
﹣3.
【解析】
试题
(1)在DE上取一点G,使DG=BF,先证:△ABF≌△ADG;再证:△AFE≌△AGE可得EF=GE,从而可得DE-EF=DE-GE=DG=BF;
(2)由AB∥CD,可得∠AED=∠BAE=30°,从而可在△ADE中求得DE=3,进而可得CE=3﹣![]() ;再由(1)△AFE≌△AGE可得∠AEF=∠AED=30°,进而可得∠CFE=90°﹣∠AEF﹣∠AED=90°﹣30°﹣30°=30°,从而可得:GE=EF=2CE=2(3﹣
;再由(1)△AFE≌△AGE可得∠AEF=∠AED=30°,进而可得∠CFE=90°﹣∠AEF﹣∠AED=90°﹣30°﹣30°=30°,从而可得:GE=EF=2CE=2(3﹣![]() )=6﹣
)=6﹣![]() ,由S△AEF=S△AGE=
,由S△AEF=S△AGE=![]() GE
GE![]() AD就可计算出所求面积.
AD就可计算出所求面积.
试题解析:
(1)在DE上取一点G,使DG=BF,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=∠ABF=90°,
在△ABF和△ADG中,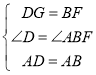 ,
,
∴△ABF≌△ADG(SAS),
∴∠DAG=∠BAF=15°,AG=AF,
∵∠EAF=45°,∠BAF=15°,
∴∠BAE=∠EAF﹣∠BAF=45°﹣15°=30°,
∴∠GAE=90°﹣15°﹣30°=45°,
∴∠GAE=∠FAE=45°,
在△AFE和△AGE中,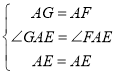 ,
,
∴△AFE≌△AGE(SAS),
∴EF=GE,
∴EF+BF=EG+DG=DE,
∴DE﹣EF=BF;
(2)∵AB∥CD,
∴∠AED=∠BAE=30°,
∴DE=![]() AD=
AD=![]() ×
×![]() =3,
=3,
∴CE=DE﹣CD=3﹣![]() ,
,
由(1)△AFE≌△AGE可得∴∠AEF=∠AED=30°,
∴∠CFE=90°﹣∠AEF﹣∠AED=90°﹣30°﹣30°=30°,
∴GE=EF=2CE=2(3﹣![]() )=6﹣2
)=6﹣2![]() ,
,
∴S△AGE=![]() (6﹣2
(6﹣2![]() )×
)×![]() =3
=3![]() ﹣3,
﹣3,
∴S△AEF=S△AGE=3![]() ﹣3.
﹣3.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过A(2,0)、C(0,12) 两点,且对称轴为直线x=4. 设顶点为点P,与x轴的另一交点为点B.
(1)求二次函数的解析式及顶点P的坐标;
(2)如图,在直线 y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?( )
A. 1条B. 2条C. 3条D. 4条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家在某小区买了一套住房,该小区楼房均为平顶式,南北朝向,楼高统一为16米(五层),小明在冬至正午测得南楼落在北楼上的影子有3.5米高(如图),且已知两楼相距有20米,请你帮小明求此时太阳光与水平线的夹角α的度数(结果精确到1°).
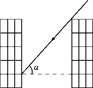
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解决后面的问题:
材料:因为二次三项式:
x2+(a+b)x+ab=(x+a)(x+b),
所以方程x2+(a+b)x+ab=0可以这样解:
(x+a)(x+b)=0,x+a=0或x+b=0,
∴x1=-a,x2=-b.
问题:
(1)(铁岭中考)如果三角形的两边长分别是方程x2-8x+15=0的两个根,那么连接这个三角形三边的中点,得到的三角形的周长可能是( )
A.5.5 B.5 C.4.5 D.4
(2)(广安中考)方程x2-3x+2=0的根是_____;
(3)(临沂中考)对于实数a,b,定义运算“﹡”:a﹡b=![]() ,例如4﹡2,因为4>2,所以4﹡2=42-4×2=8.若x1,x2是一元二次方程x2-5x+6=0的两个根,则x1﹡x2=_____;
,例如4﹡2,因为4>2,所以4﹡2=42-4×2=8.若x1,x2是一元二次方程x2-5x+6=0的两个根,则x1﹡x2=_____;
(4)用因式分解法解方程x2-kx-16=0时,得到的两根均为整数,则k的值可以为_____;
(5)已知实数x满足(x2-x)2-4(x2-x)-12=0,则代数式x2-x+1的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
(1)求弦AC的长;
(2)求证:BC∥PA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD于E,F为![]() 上一点,BF交CD于G,点H在CD的延长线上,且FH=GH.
上一点,BF交CD于G,点H在CD的延长线上,且FH=GH.

(1)求证:FH与⊙O相切.
(2)若FH=OA=5,FG=3![]() ,求AG的长.
,求AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com