
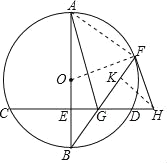
【题目】如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD于E,F为![]() 上一点,BF交CD于G,点H在CD的延长线上,且FH=GH.
上一点,BF交CD于G,点H在CD的延长线上,且FH=GH.

(1)求证:FH与⊙O相切.
(2)若FH=OA=5,FG=3![]() ,求AG的长.
,求AG的长.
【答案】(1)见解析;(2)6
【解析】
(1)连接OF,通过角之间的等量代换证明∠OFH为90°,即可得FH与⊙O相切;
(2)连接AF,作HK⊥FG于K,由FH=GH,利用等腰三角形的三线合一,可求KG,进而得出sin∠EBG等于sin∠KHG,求出AF,在直角三角形AFG中,利用勾股定理可求得AG的长.
(1)证明:连接OF,
∵FH=GH.
∴∠GFH=∠FGH,
∵∠FGH=∠BGE,
∴∠GFH=∠BGE,
∵OB=OF,
∴∠B=∠BFO,
∵AB⊥CD,
∴∠B+∠BGE=90°,
∴∠BFO+∠GFH=90°,即∠OFH=90°,
∴FH与⊙O相切;
(2)解:连接AF,作HK⊥FG于K,
∵HF=HG,HK⊥FG,
∴FK=KG=![]() ,
,
∵HF=HG,FH=OA=5,
∴HF=HG=5,
∵∠BEG=∠HKG=90°,∠BGE=∠HGK,
∴∠EBG=∠KHG,
∵AB为⊙O的直径,
∴∠AFB=90°,
∴sin∠EBG=sin∠KHG=![]() ÷5=
÷5=![]() ,
,
∴AF=![]() ,
,
∴在直角三角形AFG中,AG=![]() =6.
=6.
∴AG的长为6.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
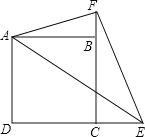
【题目】正方形ABCD中,点E在DC延长线上,点F在CB延长线上,∠EAF=45°,∠BAF=15°
(1)求证:DE﹣EF=BF;
(2)若AD=![]() ,求△AEF的面积.
,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 A、B是线段MN上的两点,MN4,MA1,MB1.以A为中心顺 时针旋转点M,以B为中心逆时针旋转点N,使MN 两点重合成一点C,构成△ABC,设ABx.(1)则x的取值范围是_________;(2)△ABC的最大面积是_________.
C 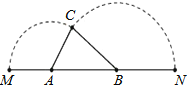
查看答案和解析>>
科目:初中数学 来源: 题型:
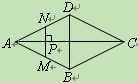
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点C、D在线段AB上,若点C是线段AD的中点,2BD>AD,则下列结论正确的是( ).
A. CD<AD- BD B. AB>2BD C. BD>AD D. BC>AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )
A. (﹣4,3) B. (﹣3,4)
C. (3,﹣4) D. (4,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知,如图①,在平行四边形ABCD中,E、F是对角线BD上的两点,且BF=DE.求证:AE=CF;
(2)已知,如图②,AB是⊙O的直径,CA与⊙O相切于点A.连接CO交⊙O于点D,CO的延长线交⊙O于点E.连接BE、BD,∠ABD=30°,求∠EBO和∠C的度数.
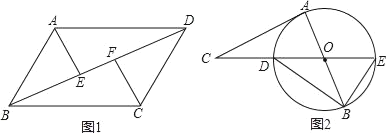
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里有四张外形相同的卡片卡片上分别标有数字﹣1,1,3,5.摸出一张后,记下数字,再放回,摇匀后再摸出一张,记下数字.以第一次得到的放字为横坐标,第二次得到的数字为纵坐标,得到一个点则这个点.恰好在直线y=﹣x+4上的概率是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com