
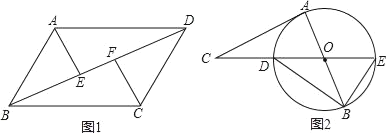
【题目】(1)已知,如图①,在平行四边形ABCD中,E、F是对角线BD上的两点,且BF=DE.求证:AE=CF;
(2)已知,如图②,AB是⊙O的直径,CA与⊙O相切于点A.连接CO交⊙O于点D,CO的延长线交⊙O于点E.连接BE、BD,∠ABD=30°,求∠EBO和∠C的度数.
【答案】(1)详见解析;(2)60°,30°.
【解析】
(1)先证明△BCF≌△DAE,再利用全等三角形的性质可得出:AE=CF;
(2)先求出∠EBO,再利用同弧所对的圆心角等于圆周角的2倍,可求出∠AOC,从而求出∠C的度数.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴∠ADE=∠FBC.
在△ADE和△CBF中,
∵AD=BC,∠ADE=∠FBC,DE=BF,
∴△ADE≌△CBF.
∴AE=CF.
(2)解:∵DE是⊙O的直径,
∴∠DBE=90°.
∵∠ABD=30°,
∴∠EBO=∠DBE﹣∠ABD=90°﹣30°=60°.
∵AC是⊙O的切线,
∴∠CAO=90°.
又∠AOC=2∠ABD=60°,
∴∠C=180°﹣∠AOC﹣∠CAO=180°﹣60°﹣90°=30°.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
(1)求弦AC的长;
(2)求证:BC∥PA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD于E,F为![]() 上一点,BF交CD于G,点H在CD的延长线上,且FH=GH.
上一点,BF交CD于G,点H在CD的延长线上,且FH=GH.

(1)求证:FH与⊙O相切.
(2)若FH=OA=5,FG=3![]() ,求AG的长.
,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
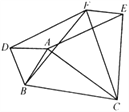
【题目】如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新美蔬菜有限公司一年四季都有大量新鲜蔬菜销往全国各地,已成为我区经济发展的重要项目。近年来它的蔬菜产值不断增加,2013年蔬菜的产值是640万元,2015年产值达到1000万元。
(1)求2014年、2015年蔬菜产值的年平均增长率是多少?
(2)若2016年蔬菜产值继续稳步增长(即年增长率与前两年的年增长率相同),那么请你估计2016年该公司的蔬菜产值将达到多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,动点D从点A出发,沿线段AC以每秒1个单位的速度向终点C运动,动点E同时从点B出发,以每秒2个单位的速度沿射线BC方向运动,当点D停止时,点E也随之停止,连结DE,当C. D. E三点不在同一直线上时,以ED、EC我邻边作ECFD,设点D运动的时间为t(秒).
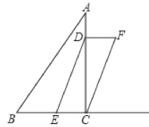
(1)用含t的代数式表示CE的长度。
(2)当F点落在△ABC的内部时,求t的取值范围。
(3)设ECFD的面积为S(平方单位),求S与t之间的函数关系式。
(4)当点F到Rt△ABC的一条直角边的距离是到另一条直角边距离的2倍时,直接写出ECFD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com