练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

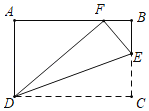
    【题目】如图，在矩形ABCD中，AB＝10，AD＝6，E为BC上一点，把△CDE沿DE折叠，使点C落在AB边上的F处，则CE的长为_____．

    【答案】

    【解析】

    设CE＝x，则BE＝6﹣x由折叠性质可知，EF＝CE＝x，DF＝CD＝AB＝10，所以AF＝8，BF＝AB﹣AF＝10﹣8＝2，在Rt△BEF中，BE2+BF2＝EF2，即（6﹣x）2+22＝x2，解得x＝．

    解：设CE＝x，则BE＝6﹣x由折叠性质可知，EF＝CE＝x，DF＝CD＝AB＝10，

    在Rt△DAF中，AD＝6，DF＝10，

    ∴AF＝8，

    ∴BF＝AB﹣AF＝10﹣8＝2，

    在Rt△BEF中，BE2+BF2＝EF2，

    即（6﹣x）2+22＝x2，

    解得x＝，

    故答案为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

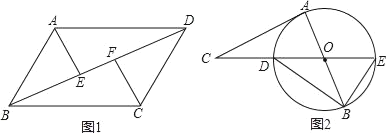
    【题目】（1）已知，如图①，在平行四边形ABCD中，E、F是对角线BD上的两点，且BF＝DE．求证：AE＝CF；

    （2）已知，如图②，AB是⊙O的直径，CA与⊙O相切于点A．连接CO交⊙O于点D，CO的延长线交⊙O于点E．连接BE、BD，∠ABD＝30°，求∠EBO和∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的箱子里有四张外形相同的卡片卡片上分别标有数字﹣1，1，3，5．摸出一张后，记下数字，再放回，摇匀后再摸出一张，记下数字．以第一次得到的放字为横坐标，第二次得到的数字为纵坐标，得到一个点则这个点．恰好在直线y＝﹣x+4上的概率是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AD＝8，AB＝4，将此矩形折叠，使点B与点D重合，折痕为EF，连接BE、DF，以B为原点建立平面直角坐标系，使BC、BA边分别在x轴和y轴的正半轴上．

    （1）试判断四边形BFDE的形状，并说明理由；

    （2）求直线EF的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y＝ax2+bx+3与x轴交于点A（﹣1，0），B（3，0）．

    （1）求抛物线的解析式；

    （2）过点D（0，）作x轴的平行线交抛物线于E，F两点，求EF的长；

    （3）当y≤时，直接写出x的取值范围是　 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

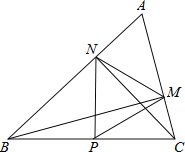
    【题目】如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，BN=PC．其中正确的个数是（）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有甲，乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克，甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同，两种机器人每小时分别搬运多少千克？设甲型机器人每小时搬运x千克，根据题意，可列方程为(　　)

    A. ＝B. ＝

    C. ＝D. ＝

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，根据图象解答下列问题：

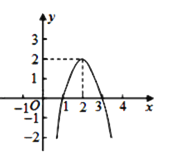
    （1）写出方程ax2+bx+c=0的两个根；

    （2）写出y随x的增大而减小的自变量x的取值范围；

    （3）若方程ax2+bx+c=k有两个不相等的实数根，求k的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，点E是AD的中点，连结BE，且BE⊥AC交AC于点F．

    （1）求证：△EAB∽△ABC；

    （2）若AD＝2，求AB的长；

    （3）在（2）的条件下，求DF的长．

    查看答案和解析>>

    同步练习册答案