练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】新美蔬菜有限公司一年四季都有大量新鲜蔬菜销往全国各地，已成为我区经济发展的重要项目。近年来它的蔬菜产值不断增加，2013年蔬菜的产值是640万元，2015年产值达到1000万元。

    （1）求2014年、2015年蔬菜产值的年平均增长率是多少？

    （2）若2016年蔬菜产值继续稳步增长（即年增长率与前两年的年增长率相同），那么请你估计2016年该公司的蔬菜产值将达到多少万元？

    【答案】（1）25%；（2）1250万元.

    【解析】

    （1）设出2014年、2015年蔬菜产值的年平均增长率是x，根据2014年蔬菜的产值×（1+年平均增长率）2=2015年产值，列方程解答即可．

    （2）利用（1）的结论即可解答．

    解：（1）设2014年、2015年蔬菜产值的年平均增长率为x，

    则有640（1+x）2=1000，

    解得：x1＝ （舍去），x2＝，

    答：2014、2015年蔬菜产值的年平均增长率为25%；

    （2）1000×（1+25%）=1250（万元）

    答：2016年该公司的蔬菜产值将达到1250万元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（6分）在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球，它们除颜色外完全相同，其中红球有2个，黄球有1个，蓝球有1个.现有一张电影票，小明和小亮决定通过摸球游戏定输赢（赢的一方得电影票）．游戏规则是：两人各摸1次球，先由小明从纸箱里随机摸出1个球，记录颜色后放回，将小球摇匀，再由小亮随机摸出1个球并记录颜色．若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏规则对双方公平吗？请你利用树状图或列表法说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，A点坐标为（3，4），将线段OA绕原点O逆时针旋转90°得到线段OA′，则点A′的坐标是（ ）

    A. （﹣4，3） B. （﹣3，4）

    C. （3，﹣4） D. （4，﹣3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

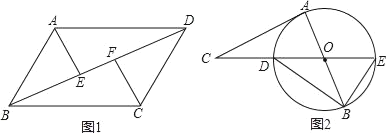
    【题目】（1）已知，如图①，在平行四边形ABCD中，E、F是对角线BD上的两点，且BF＝DE．求证：AE＝CF；

    （2）已知，如图②，AB是⊙O的直径，CA与⊙O相切于点A．连接CO交⊙O于点D，CO的延长线交⊙O于点E．连接BE、BD，∠ABD＝30°，求∠EBO和∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】调查作业：了解你所住小区家庭3月份用气量情况

    小天、小东和小芸三位同学住在同一小区，该小区共有300户家庭，每户家庭人数在2～5之间，这300户家庭的平均人数约为3.3．

    小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查，将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3．

    表1抽样调查小区4户家庭3月份用气量统计表（单位：m3）

    家庭人数

    2

    3

    4

    5

    用气量

    14

    19

    21

    26

    表2抽样调查小区15户家庭3月份用气量统计表（单位：m3）

    家庭人数

    2

    2

    2

    3

    3

    3

    3

    3

    3

    3

    3

    3

    3

    4

    用气量

    10

    11

    15

    13

    14

    15

    15

    17

    17

    18

    18

    18

    20

    22

    表3抽样调查小区15户家庭3月份用气量统计表（单位：m3）

    家庭人数

    2

    2

    2

    3

    3

    3

    3

    3

    3

    4

    4

    4

    4

    5

    5

    用气量

    10

    12

    13

    14

    17

    17

    18

    20

    20

    21

    22

    26

    31

    28

    31

    根据以|材料回答问题：

    （1）小天、小东和小芸三人中，哪位同学抽样调查的数据能较好地反映出该小区家庭3月份用气量情况？请简要说明其他两位同学抽样调查的不足之处．

    （2）在表3中，调查的15个家庭中使用气量的中位数是　 　m3，众数是　 　m3．

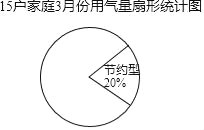
    （3）小东将表2中的数据按用气量x（m3）大小分为三类．

    ①节约型：10≤x≤13，②适中型：14≤x≤17，③偏高型：18≤x≤22，并绘制成如图扇形统讣图，请帮助他将扇形图补充完整．

    （4）小芸算出表3中3月份平均每人的用气量为6m3，请估计该小区3月份的总用气量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们将使得函数值为零的自变量的值称为函数的零点值，此时的点称为函数的零点．例如，对于函数，令，可得，我们就说1是函数的零点值，点是函数的零点．

    已知二次函数．

    （1）若函数有两个不重合的零点时，求k的取值范围；

    （2）若函数的两个零点都是整数点，求整数k的值；

    （3）当k<0时，在（2）的条件下，函数的两个零点分别是点A，B（点A在点B的左侧），将二次函数的图象在点A，B间的部分（含点A和点B）向左平移个单位后得到的图象记为，同时将直线向上平移个单位．请结合图象回答：当平移后的直线与图象有公共点时，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

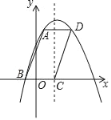
    【题目】如图，ABCD与抛物线y＝﹣x2+bx+c相交于点A，B，D，点C在抛物线的对称轴上，已知点B（﹣1，0），BC＝4．

    （1）求抛物线的解析式；

    （2）求BD的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的箱子里有四张外形相同的卡片卡片上分别标有数字﹣1，1，3，5．摸出一张后，记下数字，再放回，摇匀后再摸出一张，记下数字．以第一次得到的放字为横坐标，第二次得到的数字为纵坐标，得到一个点则这个点．恰好在直线y＝﹣x+4上的概率是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有甲，乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克，甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同，两种机器人每小时分别搬运多少千克？设甲型机器人每小时搬运x千克，根据题意，可列方程为(　　)

    A. ＝B. ＝

    C. ＝D. ＝

    查看答案和解析>>

    同步练习册答案