
【题目】【阅读】
如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(1)【理解】
若点D与点A重合,则这个操作过程为FZ[ , ];
(2)【尝试】
若点D恰为AB的中点(如图2),求θ;
(3)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(4)【探究】
经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].
【答案】
(1)45°;3
(2)
解:如答图1所示,连接CD并延长,交x轴于点F.

在△BCD与△AFD中,
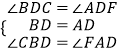
∴△BCD≌△AFD(ASA).
∴CD=FD,即点D为Rt△COF斜边CF的中点,
∴OD= ![]() CF=CD.
CF=CD.
又由折叠可知,OD=OC,
∴OD=OC=CD,
∴△OCD为等边三角形,∠COD=60°,
∴θ= ![]() ∠COD=30°
∠COD=30°
(3)
解:经过FZ[45°,a]操作,点B落在点E处,则点D落在x轴上,AB⊥直线l,
如答图2所示:

若点E在四边形0ABC的边AB上,
由折叠可知,OD=OC=3,DE=BC=2.
∵AB⊥直线l,θ=45°,
∴△ADE为等腰直角三角形,
∴AD=DE=2,
∴OA=OD+AD=3+2=5,
∴a=5;
由答图2可知,当0<a<5时,点E落在四边形0ABC的外部
(4)
FZ[30°,2+ ![]() ],FZ[60°,2+
],FZ[60°,2+ ![]() ].
].
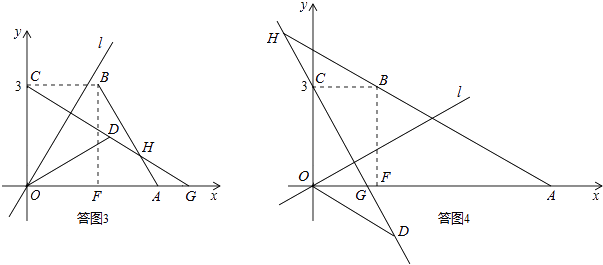
如答图3、答图4所示.
【解析】解:【理解】
若点D与点A重合,由折叠性质可知,OA=OC=3,θ= ![]() ∠AOC=45°,
∠AOC=45°,
∴FZ[45°,3].
【理解】由折叠性质可以直接得出.【尝试】(2)如答图1所示,若点D恰为AB的中点,连接CD并延长交x轴于点F.证明△BCD≌△AFD,进而得到△OCD为等边三角形,则θ=30°;(3)如答图2所示,若点E在四边形0ABC的边AB上,则△ADE为等腰直角三角形,由此求出a=OA=OD+OA=5;由答图2进一步得到,当0<a<5时,点E落在四边形0ABC的外部.【探究】满足条件的图形有两种,如答图3、答图4所示,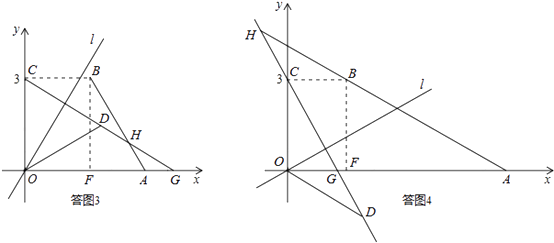


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在函数y1=﹣ ![]() (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点M在以O为圆心,AB为直径的半圆弧上运动(点M不与点A、B 及 ![]() 的中点F 重合),连接OM.过点M 作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连接BM、BN.
的中点F 重合),连接OM.过点M 作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连接BM、BN.
(1)探究:如图一,当动点M在 ![]() 上运动时;
上运动时;
①判断△OEM∽△MDN是否成立?请说明理由;
②设 ![]() =k,k是否为定值?若是,求出该定值,若不是,请说明理由;
=k,k是否为定值?若是,求出该定值,若不是,请说明理由;
③设∠MBN=α,α是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如图二,当动点M 在 ![]() 上运动时;
上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家环保局统一规定,空气质量分为5级.当空气污染指数达0﹣50时为1级,质量为优;51﹣100时为2级,质量为良;101﹣200时为3级,轻度污染;201﹣300时为4级,中度污染;300以上时为5级,重度污染.泰州市环保局随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题: 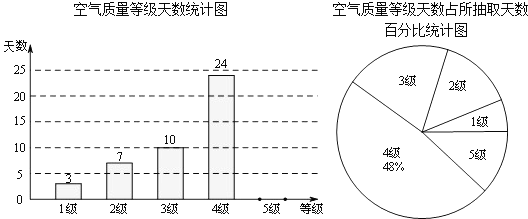
(1)本次调查共抽取了天的空气质量检测结果进行统计;
(2)补全条形统计图;
(3)扇形统计图中3级空气质量所对应的圆心角为°;
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.为了了解学生和家长对中学生带手机的态度,某记者随机调查了城区若干名学生和家长的看法,调查结果分为:赞成、无所谓、反对,并将调查结果绘制成如下不完整的统计表和统计图:学生及家长对中学生带手机的态度统计表
对象 | 赞成 | 无所谓 | 反对 |
学生 | 80 | 30 | 90 |
家长 | 40 | 80 | A |

根据以上图表信息,解答下列问题:
(1)统计表中的A.
(2)统计图中表示家长“赞成”的圆心角的度数
(3)从这次接受调查的学生中,随机抽查一个,恰好是持“反对”态度的学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论: ①∠AFC=120°;
②△AEF是等边三角形;
③AC=3OG;
④S△AOG= ![]() S△ABC
S△ABC
其中正确的是 . (把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO是平行四边形,点C在x轴的负半轴上,AO=2cm,AB=4cm,∠BAO=60°,将ABCO绕点A逆时针旋转60°,得到对应的ADEF,解答下列问题: 
(1)画出旋转后的ADEF(不写作法,不证明,保留作图痕迹);
(2)求ABCO旋转过程中扫过的区域的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com